BOS Abschlussprüfung 2007: Lineare Algebra

Abschlussprüfung zur Erlangung der fachgebundenen Hochschulreife
Frühjahr 2007

Aufgabengruppe B: B I B II

B I

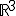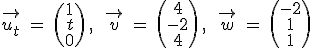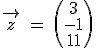1.0	Im sind die Vektoren und mit 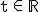sowie die drei Ebenen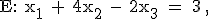 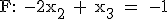und 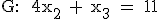gegeben.

1.1	Bestimmen Sie die Werte von t, für welche die drei Vektoren 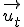, , 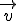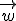eine Basis des 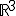bilden und ermitteln Sie für t = 0 eine Darstellung von 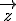als Linearkombination der Vektoren 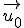, , 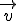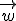. (7 BE)

1.2	Weisen Sie (eventuell unter Verwendung der Aufgabe 1.1) nach, dass sich die drei Ebenen E, F und G in genau einem Punkt schneiden und bestimmen Sie die Koordinaten dieses Punktes. Schließen Sie unter anderem daraus auf die gegenseitige Lage der Ebenen F und G und ermitteln Sie, falls möglich, die Koordinaten dreier gemeinsamer Punkte von F und G. (6 BE)

1.3	Eine der unten angegebenen Zeichnungen gibt die gegenseitige Lage der Ebenen E und G sowie der 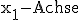an. Begründen Sie, welche Zeichnung richtig ist. (3 BE)


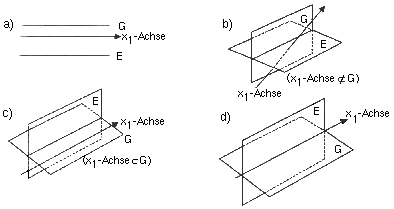
2	Geben Sie je eine Gleichung einer Ebene H in Parameterform und in Koordinatenform an, die keine Koordinatenebene ist und die mit der 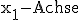mehr als einen Punkt gemeinsam hat. (4 BE)


3.0	Ein bestimmtes Unternehmen lässt sich in drei Werke U, V und W unterteilen. Diese sind untereinander und mit dem Markt nach dem Leontief-Modell verflochten. Die Gesamtproduktion dieses Jahres in Werk U beträgt 100 ME, in Werk V 40 ME und in Werk W 50 ME. Die Inputmatrix ist gegeben durch .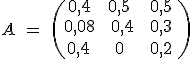

3.1	Bestimmen Sie die Input-Output-Tabelle dieses Jahres. (4 BE)

3.2	Nach Meinung eines Experten ist im nächsten Jahr der Konsumvektor 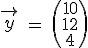zu erwarten. Ermitteln Sie den zugehörigen Produktionsvektor . (5 BE)


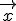3.3.0	Analysen haben gezeigt, dass die Kapazität der Werke U und W nur unter unverhältnismäßig großem finanziellem Aufwand erhöht werden kann. Deshalb will man nur bei der Produktion des Werkes V etwas ändern, die Produktion der Werke U und W aber bei 100 ME bzw. 50 ME belassen.

3.3.1	Bestimmen Sie das Intervall, in welchem die Produktion im Werk V möglich ist. (5 BE)

3.3.2	Die Produktionskosten für jeweils eine produzierte Mengeneinheit (ME) betragen im Werk U 4 Geldeinheiten (GE), im Werk V 6 GE und im Werk W 8 GE. Beim Verkauf einer ME am Markt erzielt man als Erlös das Zwanzigfache der jeweiligen Produktionskosten (unterschieden je nach Werk). Zeigen Sie, dass sich für den gesamten Marktverkaufserlös 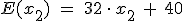ergibt, wenn Sie davon ausgehen, dass alles am Markt Angebotene auch wirklich verkauft wird. (2 BE)

3.3.3	Unter der Voraussetzung von 3.3.0 gilt für die Produktion von Werk V 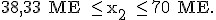Bestimmen Sie, für welchen Wert von 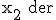höchste Gesamtgewinn G (G = Erlös – Kosten) erzielt wird und geben Sie diesen höchsten Gesamtgewinn an. Begründen Sie Ihre Antwort. (4 BE)

B II

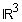1.0 Im sind die Punkte  A_a ( a ; 1 + 4a ; -2 - a ) , B ( 1 ; 1 ; -1 ) und C ( -2 ; 4 ; 8 ) sowie
      die Ebenen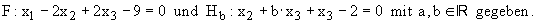 

1.1 Weisen Sie nach, dass der Punkt B nicht zur Menge der Punkte A_a gehört und beschreiben Sie
       geometrisch die Punktmenge A_a .      ( 3 BE )

1.2 Die Punkte A_a und B legen eine Ebene E fest. Ermitteln sie eine Koordinatengleichung dieser Ebene.
       (Mögliches Ergebnis : 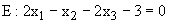   )       ( 5 BE )

1.3 Die Gerade 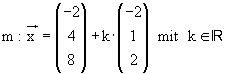 schneidet die Ebene E im Punkt S.
      Berechnen Sie die Koordinaten von S sowie die Koordinaten des Spiegelpunktes C^*von C an S.
      Ermitteln Sie außerdem die Koordinaten eines Punktes D auf der Geraden m , der vom Punkt S nur
      ein Drittel so weit entfernt ist wie C.
      (Teilergebnis : S ( 4 ; 1 ; 2 )  )        ( 6 BE )

1.4 Beschreiben Sie in Abhängigkeit von b die besondere Lage der Ebenen H_b im Koordinatensystem.     ( 3 BE )

1.5 Bestimmen Sie eine Gleichung der Schnittgeraden s der beiden Ebenen E (aus 1.2) und F.
      Ermitteln Sie außerdem den Wert von b , für den die Ebenen E, F und H_b keinen gemeinsamen Punkt haben.
      ( Mögliches Teilergebnis : 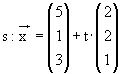  )        ( 6 BE )


2.0 Die drei Werke W1, W2 und W3 eines Unternehmens erzeugen verschiedene Grundstoffe.
      Sie sind untereinander und mit dem Markt nach dem Leontief-Modell verflochten.
      Die Bedarfsbeziehungen sowie die jeweilige Gesamtproduktion sind in untenstehender Tabelle (in Mengen-
      einheiten ME) erfasst.
      

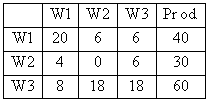2.1 Erstellen Sie die Inputmatrix A und bestimmen Sie den Marktvektor.     ( 4 BE )

2.2 W1 und W3 sollen ihre Abgabe an den Markt auf 60 ME, W2 auf 48 ME erhöhen.
      Berechnen Sie die dazu notwendige Produktion der einzelnen Werke.   ( 6 BE )

2.3 Über einen längeren Zeitraum muss die Produktion von W2 auf 30 ME gedrosselt werden.
      W1 soll dafür 50% mehr produzieren als W3. W3 ist variabel.
      Bestimmen Sie in welchem Intervall sich die Produktion von W3 bewegen muss, um sinnvolle Werte für die Markt-
      abgabe zu realisieren. Prüfen Sie, ob es unter diesen Rahmenbedingungen möglich ist, dass W1 weniger an den Markt
      abgibt als W2.     ( 7 BE )