Prüfung zur Erlangung der fachgebundenen Hochschulreife
Frühjahr 1999

Aufgabengruppe B:   B I   B II

B I

1.

In einem kartesischen Koordinatensystem sind die Punkte  A( 3 | 2 | 1 ), 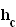  B( 4 | 4 | 3 )  und  C ( 5 | 0 | 5 )   sowie die Schar von Geraden    durch 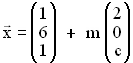   mit  c IR  und  m IR  gegeben.

1.1    

Die Ebene E₁ enthält die Punkte A, B und C. Bestimmen Sie jeweils eine Gleichung der Ebene E₁ in Parameterform und in parameterfreier Darstellung.   (5 BE)
( Zur Kontrolle: E₁:  2x₁ – x₃ – 5 = 0 )

1.2

Untersuchen Sie, für welche Werte von  c  die Gerade  h_c  parallel zur Ebene  E₁  verläuft, aber nicht in  E₁  enthalten ist.   (5 BE)

1.3

Nun sei  c = 2.  Zeigen Sie, dass der Schnittpunkt  S  der Geraden  h₂  mit der Ebene  E₁  auf der Geraden durch die Punkte  A  und  B  liegt. Berechnen Sie, in welchem Verhältnis der Punkt  S  die Strecke  [AB]  teilt und folgern Sie daraus eine Aussage über die Lage des Punktes  B  bezüglich  [AS].   (8 BE)
( Zur Kontrolle: S( 5 | 6 | 5 ) )

1.4

Die Ebene  E₂  enthält den Koordinatenursprung und die Gerade  h₂.  Ermitteln Sie eine Gleichung der Schnittgeraden der Ebenen  E₁  und  E₂.   (6 BE)

2.

Gegeben sind die reellen Matrizen
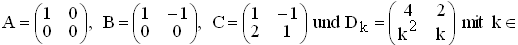IR .

2.1

Ermitteln Sie den Wert des Parameters  k,  für den die Produktmatrix  B · D_k  die Nullmatrix ist.   (3 BE)

2.2

Überprüfen Sie rechnerisch, ob das Matrizenprodukt  B · D_k  kommutativ ist.   (3 BE)

2.3

Untersuchen Sie, für welche Werte des Parameters  k  die vier Matrizen  A,  B,  C,  D_k eine Basis des Vektorraums der reellen (2,2)-Matrizen bezüglich der üblichen Verknüpfungen  „+“  und  „·“  bilden.   (7 BE)

2.4

Nun sei  k = 3.  Berechnen Sie die Koordinaten der Matrix  F = 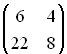  bezüglich der Basis  A,  B,  C  und  D.   (3 BE)

B II

1.

Über das Alter von vier Personen  A,  B,  C  und  D  in ganzen Jahren liegen folgende Aussagen vor: Die vier Personen sind zusammen 100 Jahre alt.  A  und  C  sind zusammen genau so alt wie  B  und  D  zusammen. Vor 10 Jahren waren  A  und  D  zusammen so alt wie  B  heute.

1.1

Stellen Sie diese Zusammenhänge in einem Gleichungssystem dar und bestimmen Sie die Lösungsmenge dieses Gleichungssystems in Abhängigkeit vom Alter  d  der Person D. Erläutern Sie, dass nur wenige ganzzahlige Werte für  d  möglich sind.   (7 BE)

1.2

Ermitteln Sie die eindeutige Lösung des Gleichungssystems, wenn zusätzlich bekannt ist, dass in  5  Jahren  B  viermal so alt sein wird, wie  D  vor  5  Jahren war.   (3 BE)

2.

Drei Wirtschaftssektoren  R,  S  und  T  sind nach dem Leontiefmodell miteinander und mit dem Markt verbunden. Gegeben sind die Input-Matrix    und der Produktionsvektor  .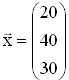

2.1

Erstellen Sie die zugehörige Input-Output-Tabelle, die auch den Konsumvektor enthält.   (4 BE)

2.2

Die Produktion des Sektors  R  soll um  a  Einheiten erniedrigt werden, während die Produktionseinheiten bei  S  und bei  T  konstant bleiben sollen. Bestimmen Sie den maximal möglichen Wert von  a.   (6 BE)

2.3

Durch eine Umorganisation in Sektor T wurde erreicht, dass sich der Koeffizient 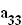 verändert. Dadurch ergibt sich für den Produktionsvektor 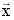aus obiger Angabe, dass von Sektor T  7 Einheiten auf den Markt kommen. Ermitteln Sie die Marktabgaben von  R  und  S  sowie den Koeffizienten  a₃₃ , und erläutern Sie kurz dessen Bedeutung.   (6 BE)

3.

Die Punkte  A( 1 | 1 | 4 ),  B( –1 | 2 | 8 )  und  C( 5 | 1 | 0 )  legen die Ebene  E  fest, die Punkte  P( 6 | 1 | 2 )  und  Q( 1 | 6 | 12 )  liegen auf der Geraden  g.

3.1

Bestimmen Sie eine Gleichung von  E  in vektorieller Form sowie in parameterfreier Darstellung.   (5 BE)
(Mögliches Ergebnis:  E:  x₁ – 2x₂ + x₃ – 3 = 0 )

3.2

Geben Sie eine Gleichung der Geraden  g  an, und bestimmen Sie die Koordinaten des Schnittpunktes  T  von  g  mit  E.   (4 BE)

3.3

Berechnen Sie das Teilverhältnis, in dem der Punkt  T( 3 | 4 | 8 )  die Strecke  [PQ]  teilt. Begründen Sie anhand einer Skizze, welcher der Punkte  P  oder  Q  demnach näher an der Ebene  E  liegt.   (5 BE)