Seminararbeit von
Markus Böhm, Januar 2005
Seminararbeit von
Markus Böhm, Januar 2005
Gliederung
a.
Addition von gleichnamigen Bruchtermen
b. Subtraktion von
gleichnamigen Bruchtermen
a.
Multiplikation von Bruchtermen
b. Division von Bruchtermen
Begriffserklärung
Was ist ein Bruch?
Ein Bruch wird aus zwei ganzen Zahlen (...3, 2, 1, 0, -1, -2, -3,...), die
übereinandergestellt sind, gebildet. Diese sind durch einen waagerechten
Strich getrennt. Die obenstehende Zahl nennt man Zähler, die untenstehende
Nenner.
Bruch: z. B. 
Was ist ein Term?
Unter einem Term versteht man Zahlzeichen,
Variablen sowie
alle sinnvollen Verbindungen von Zahlenzeichen und Variablen mit Verknüpfungszeichen.
Term: z. B. x+3
Was ist ein Bruchterm?
Der aus den zwei Termen erstellte Bruch 
heißt
Bruchterm.
Bruchterm: z. B. 
Erweitern
von Bruchtermen
Ein Bruchterm wird erweitert, indem man seinen Zähler und Nenner mit demselben
Term multipliziert.
Beim Erweitern bleibt der Wert des Bruches erhalten!
Beispiel:
mit 3x erweitern
Kürzen
von Bruchtermen
Ein Bruch wird gekürzt, indem man seinen Zähler und Nenner mit demselben
Term dividiert.
Auch beim Kürzen bleibt der Wert des Bruches erhalten!
Beispiel:
mit
4x kürzen
Gleichnamigmachen
von Bruchtermen
Gleichnamig bedeutet, dass die jeweiligen Bruchterme den gleichen
Nenner haben. Um allerdings zu diesem Ergebnis zu gelangen, muss der kleinste
gemeinsame Vielfache aus den gegebenen Nennern ermittelt werden.
Beispiel:
und 
haben als kleinstes gemeinsames Vielfaches den Hauptnenner 2x²- 18.
Das ergibt sich aus der Faktorzerlegung der einzelnen Nenner 2(x-3) und
(3-x)(3+x).
Nun muss
mit (x+3) und
mit (-2) erweitert werden.
und
Als Alternativlösung bietet sich aber auch das Multiplizieren mit dem jeweils
anderen Nenner an.
Da ist man immer auf dem richtigen Weg! 
(Es kann aber zu ziemlich großen Termen führen.)
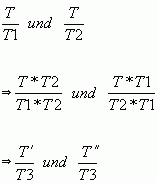
Beispiel:
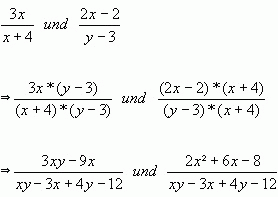
a.
Addition von gleichnamigen Bruchtermen
Gleichnamige Bruchterme werden addiert, indem man die Terme im Zähler addiert
und den Term im Nenner beibehält.
Beispiel:
b.
Subtraktion von gleichnamigen Bruchtermen
Gleichnamige Bruchterme werden subtrahiert, indem man die Terme im Zähler
subtrahiert und den Term im Nenner beibehält.
Beispiel:
Addition
und Subtraktion von ungleichnamigen Bruchtermen
Ungleichnamige Bruchterme müssen zuerst gleichnamig gemacht werden (siehe
Punkt 4). Dann wird wie unter Punkt 5 weiterverfahren.
Beispiel Addition:
Beispiel Subtraktion:
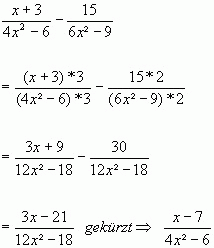
a.
Multiplikation von Bruchtermen
Vor dem Ausmultiplizieren ist es zu empfehlen, dass Zähler und Nenner möglichst
vollständig gekürzt werden.
Zwei Bruchterme werden multipliziert, indem man Zähler mit Zähler und Nenner
mit Nenner multipliziert.
Beispiel:
Kleiner Tip: Es kann ausgeklammert und gekürzt werden.
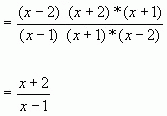
b.
Division von Bruchtermen
Man dividiert durch einen Bruchterm, indem man den Dividenden (=
erster Bruch) mit dem Kehrbruch des Divisors (= zweiter Bruch) multipliziert.
Beispiel:
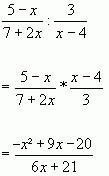
Bruchgleichungen
Bei Bruchtermen
können im Zähler UND im Nenner Variablen vorkommen. Da die Division
durch die Zahl Null leider keinen Sinn ergibt, ist es besonders wichtig,
die Definitionsmenge bei Bruchgleichungen zu bestimmen, die Werte, die beim
Einsetzen in die Variablen dem Nenner den Wert Null geben!
Daran denken: Bei der Bestimmung der Definitionsmenge
nur den Nenner anschauen!
Beispiel:
Hier darf man für x alle Reellen
Zahlen außer 0 einsetzen.
In der Mathematik schreibt man D=R \ {0}
Übersetzt heißt das:
Die Definitionsmenge D sind alle Reellen Zahlen R außer
der Menge mit der Zahl 0!
Beispiel:
Hier darf man für x alle Reellen Zahlen außer -3 einsetzen, denn
-3+3=0
D=R \ {-3}
Strategie bei der Lösung von Bruchgleichungen:
1.) Defintionsmenge festlegen
2.) Hauptnenner bestimmen
3.) Beide Seiten mit dem Hauptnenner multiplizieren
4.) Durch Kürzen eine lineare (oder quadratische) Gleichung erzeugen
5.) Gleichung durch eine Äquivalenzumformung
lösen
6.) Bei der Bestimmung der Lösungsmenge die Definitionsmenge beachten
Beispiel:
D=R \ {0} ; Hauptnenner: x
