| 11. Klasse |
1. Schulaufgabe |
07.12.2006 |
| Gruppe B |
Arbeitszeit 65 min |
|
| |
| 1a |
Erst müssen bei dieser Gleichung die Klammern auf beiden Seiten aufgelöst werden. Dabei muss beachtet werden, dass sich die Vorzeichen ändern, wenn Minus vor einer Klammer steht. Dann können alle Terme mit b zusammengefasst werden, ebenso alle Zahlen, zum Schluss muss nach b aufgelöst werden. |
 |
| |
|
 |
| 1b |
Bei dieser Gleichung müssen erst alle Klammern ausmultipliziert werden, dabei sollten die Binome beachtet werden. Weiter wie oben. |
|
| |
|
|
| |
|
|
| |
|
|
| 2. |
Bei dieser Aufgabenstellung muss -2 für jedes x in der Gleichung eingesetzt werden. Wenn dies geschehen ist, werden die Werte der beiden Seiten berechnet. Das Ergebnis auf der linken und rechten Seite des Gleichheitszeichens ist nicht identisch und somit ist -2 keine Lösung dieser Gleichung. |

|
| |
|
 |
| |
|
|
| 3. |
Gegeben ist der Term |
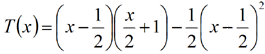 |


|
| 3a |
Hier muss die Zahl 0 für x eingesetzt werden. Dann müssen die Klammern ausgerechnet und aufgelöst werden. "Hoch vor Punkt vor Strich"-Regel beachten. |
|
| |
Nochmal die gleiche Rechnung, nur dass nun 1/2 eingesetzt wird. Das besondere dabei liegt an dem Term 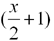 . Wenn man hier 1/2 für x einsetzt, erhält man einen Doppelbruch, der mittels Kehrwertmethode aufgelöst wird. . Wenn man hier 1/2 für x einsetzt, erhält man einen Doppelbruch, der mittels Kehrwertmethode aufgelöst wird. |
|
| |
|
|
| 3b |
Die Klammern werden ausmultipliziert (Binom!) und dann gleichartige Terme zusammengefasst. |
|
| |
|
|
| |
|
|
| 4 |
|

|
| |
a) Der Zähler enthält das erste Binom und im Nenner kann die 2 ausgeklammert werden . In Zähler und Nenner steht dann jeweils ein Faktor (3x+2). Dieser kann weggekürzt werden. |
 |
| |
b) Im Zähler kann 2x ausgeklammert werden und im Nenner ist die 3. Binomische Formel enthalten. Im Zähler und Nenner steht nun jeweils ein Faktor (1-2x). Dieser kann weggekürzt werden. |
|
| |
c) Erst kann in Zähler und Nenner 3x ausgeklammert und gekürzt werden. Dann kann im Zähler nochmal x ausgeklammert und im Nenner die 3. binomische Formel angewendet werden. Der Faktor (x-3) kann weggekürzt werden.
|
|
| 5. |
Aus dem Angabentext ergibt sich, dass die drei Anteile nicht bekannt sind und berechnet werden müssen. Die Aussagen beziehen sich auf Lisas Anteil, also wird dieser gleich x gesetzt. Da sie Marens Auto benutzten, muss diese 50 Euro weniger bezahlen, somit x-50. Katrin war krank und muss 25% weniger bezahlen, also x-(25% von x), d.h. x - 1/4 x oder 3/4 x.
Nun hat man 3 Terme, die zusammen den Endbetrag 280 Euro ergeben. Man löst nach x auf, und kann nun die Anteile der drei Mädchen berechnen. |


|
| |
|
|
| |
|
|
| 6. |
 |

|
| 6a |
Das Trapez kann aufgeteilt werden in 2 Dreiecke und ein Rechteck. Die Dreiecke sind gleich groß.Die allgemeine Flächeninhaltsformel des Dreicks lautet: A = 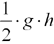 . Nun kann man die Werte des Dreicks einsetzen. Man erhält den Flächeninhalt in Abhängigkeit von b. . Nun kann man die Werte des Dreicks einsetzen. Man erhält den Flächeninhalt in Abhängigkeit von b.
Beim Rechtecks multipliziert man Länge und Breite und erhält den Flächeninhalt in Abhängigkeit von a.
Nun kann man den Flächeninhalt von beiden Dreiecken und dem Rechteck zusammenzählen und soweit wie möglich vereinfachen.
Beim Umfang addiert man die Längen der Außenlinien und vereinfacht soweit wie möglich. |
 |
| |
|
|
| 6b |
Man setzt nun für a=5 ein und setzt die Flächeninhaltsformel des Trapezes aus 6a) mit 57 gleich. Somit erhält man das gesuchte b. |
|
| |
|
|
| |
|
|
| |
|
|
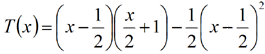
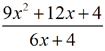

![]() . Nun kann man die Werte des Dreicks einsetzen. Man erhält den Flächeninhalt in Abhängigkeit von b.
. Nun kann man die Werte des Dreicks einsetzen. Man erhält den Flächeninhalt in Abhängigkeit von b.