|
|
|
|
|
| |
|
|
|
|
| 1. |
Geben Sie möglichst viele Informationen an, die Sie aus den folgenden Funktionsgleichungen ablesen können, ohne eine Rechnung auszuführen. |
|
|
|
| a) |
f(x) = 14 (x - 2)² + 9 |
|
|
|
| b) |
f(x) = - 0,3 (x - 2) (x + 4) |
|
|
|
| c) |
f(x) = 2x - 5 |
|
(7) |
|
| |
|
|
|
|
| |
|
|
|
|
| 2. |
Gegeben ist eine Parabel mit der Gleichung p(x) = 4 x² - 20x - 7,5 |
|
|
|
| |
|
|
|
|
| 2.1 |
Wandeln Sie die Parabelgleichung in die Scheitelform um. |
|
|
|
| |
|
|
|
|
| 2.2 |
Zeigen Sie rechnerisch, dass die Parabel die x-Achse zweimal schneidet. |
|
(6) |
|
| |
|
|
|
|
| |
|
|
|
|
| 3. |
Gegeben ist die Gerade g: y = - x - 1,5 und die parameterabhängige Parabelgleichung pc(x) = 0,5 x² + 2x + c |
|
|
|
| |
|
|
|
|
| 3.1 |
Zeichnen Sie die Gerade und die zu c = 2 gehörende Parabel in ein geeignetes Koordinatensystem. Berechnen Sie für welche Werte von x die Parabel oberhalb der Geraden verläuft. |
|
|
|
| |
|
|
|
|
| 3.2 |
Bestimmen Sie c so, dass die Parabel die Gerade g berührt. Berechnen Sie auch den Berührpunkt. |
|
(18) |
|
| |
|
|
|
|
| |
|
|
|
|
| 4. |
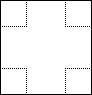
Für die Verpackung von Schokobonbons soll eine nach oben offene Papierkiste hergestellt werden. Dafür steht quadratisches Papier von 25 cm Seitenlänge zur Verfügung. Die Seitenflächen sollen mit Produktinformationen bedruckt werden und deshalb nicht zu klein sein.
 |
|
|
|
| |
|
|
|
|
| 4.1 |
Wie groß wird eine Seitenfläche, wenn man die Pappe 2 cm tief einschneidet? |
|
|
|
| |
|
|
|
|
| 4.2 |
Geben Sie die Grösse einer Seitenfläche in Abhängigkeit von der Einschnitttiefe x an. (Zwischenergebnis A(x) = 25x - 2 x²). |
|
|
|
| |
Wie ist die Einschnitttiefe zu wählen, damit die Seitenfläche möglichst groß wird? |
|
|
|
| |
Geben Sie auch den Fächeninhalt dieser Seitenfläche an. |
|
(7) |
|
| |
|
|
|
|
| |
|
|
|
|
| 5. |
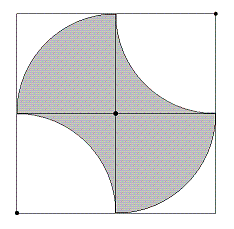
Berechnen Sie den Flächeninhalt und den Umfang der getönten Fäche. Die Mittelpunkte der einzelnen Kreisbögen sind markiert, der Radius der Kreisboegen ist a. |
|
(6) |
|
| |
 |
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
 |
|
|
|
| |
|
|
|
|
| |
|
|
|
|

