1. Gegeben ist die reelle Funktion f: x
f(x),
f(x) =
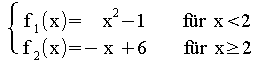
Überprüfen Sie rechnerisch, ob die Funktion f an der Stelle x 0 =
2 stetig ist.
1) Vorüberlegung:
f1 (x0) muss gleich f2 (x0) sein,
damit die Funktion f(x) an der Nahtstelle x0= 2 stetig ist.
2) Funktionswerte für x0= 2 ausrechnen:
und
3) Schlussfolgerungen:
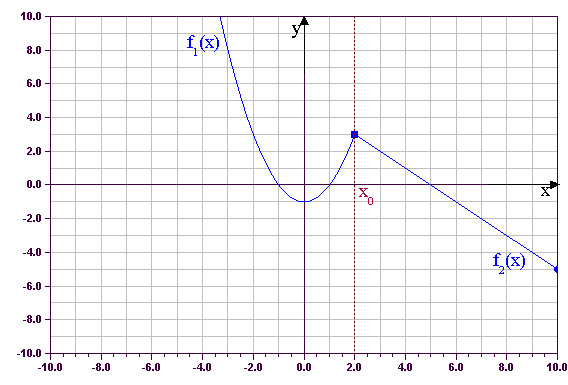
, somit ist die Funktion f(x) an der Nahtstelle x0 unstetig
und ihr Graph Gf weist eine „Sprungstelle“ auf.
4) graphische Darstellung:
2. Gegeben ist die reelle Funktion f: xf(x),
f (x) =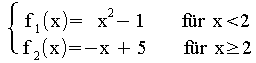
Überprüfen sie rechnerisch, ob die Funktion f an der Stelle x0= 2
stetig ist.
Lösung:
Stetigkeit prüfen:
Es muss gelten: 
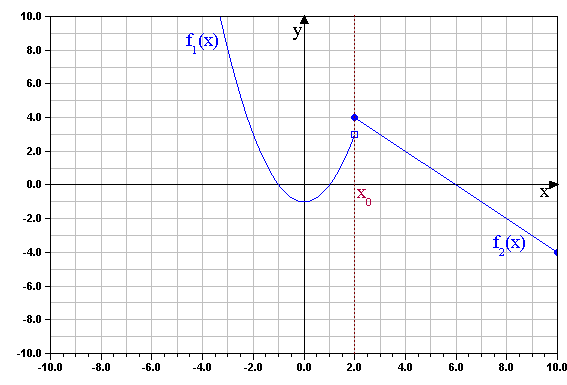
f(x) ist an der Stelle x0= 2 stetig
Der Graph Gf hat an der Nahtstelle x0 keinen „Sprung“.
graphische Darstellung:
