Allgemeine Definition für Differenzierbarkeit:
Eine stetige Funktion f(x) ist an der Stelle
genau dann differenzierbar,
wenn gilt:
In eigenen Worten bedeutet dies:
Der Grenzwert der Ableitungsfunktion f '(x) für x gegen x0 muss gleich dem
Funktionswert der Ableitungsfunktion an der Stelle x0 sein,
d.h. sowohl linksseitig für x < x0 als auch rechtsseitig für x > x0 .
Vorraussetzung für die Differenzierbarkeit einer Funktion an der Stelle x0
ist also die Stetigkeit dieser Funktion an der Stelle x0 .
Übertragung der allg. Def. für Differenzierbarkeit auf abschnittsweise definierte
Funktionen:
Bei abschnittsweise definierten Funktionen f (x) =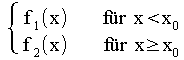
ändert sich definitionsbedingt an der Nahtstelle x0 der Funktionsterm, somit müssen
die Grenzwerte der Ableitungsfunktion f '(x) sowohl für x < x0 als auch für x > x0
mit dem jeweilig definierten und abgeleiteten Funktionsterm, also mit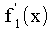
und mit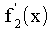
, berechnet werden. Diese müssen
laut allgemeiner Definition für
die Differenzierbarkeit mit dem Funktionswert der Ableitungsfunktion an der
Nahtstelle x0 übereinstimmen.
Auch hier gilt: linksseitiger Grenzwert ist f1'(x0), rechtsseitiger ist f2'(x0).
Somit ist eine abschnittsweise definierte Funktion f(x) an der Nahtstelle x0
differenzierbar, wenn gilt:
1)
2)
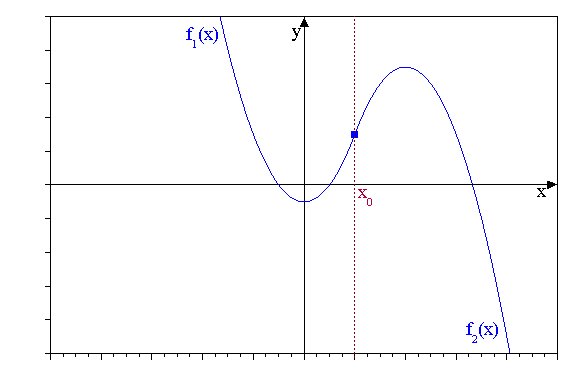
Für den Graphen einer Funktion bedeutet dies, dass er keine „Sprungstelle“ und
keinen „Knick“ aufweist, wie im folgenden Beispiel dargestellt.
