genau dann stetig, wenn gilt:
Stetigkeit:
Allgemeine Definition für Stetigkeit:
Eine Funktion f(x) ist an der Stellegenau dann stetig, wenn gilt:
In eigenen Worten bedeutet dies:
Der Grenzwert der Funktion f(x) für x gegen x0, d.h. sowohl der linksseitige
für x < x0 als auch der rechtsseitige für x > x0 , muss gleich dem Funktionswert an
der Nahtstelle x0 sein.
Übertragung der allg. Def. für Stetigkeit auf abschnittsweise definierte Funktionen:
Bei abschnittsweise definierten Funktionen f(x) =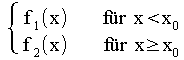
ändert sich definitionsbedingt an der Nahtstelle x0 der Funktionsterm, somit müssen
die Grenzwerte der Funktion f(x) sowohl für x < x0 als auch für x > x0 mit dem
jeweilig definierten Funktionsterm, also mit f1(x) und mit f2(x), berechnet werden.
Diese müssen laut allgemeiner Definition für die Stetigkeit mit dem Funktionswert
an der Nahstelle x0 übereinstimmen.
Dabei ist der linksseitige Grenzwert gleich f1(x0), der rechtsseitige gleich f2(x0).
Somit ist eine abschnittsweise definierte Funktion f(x) an der Nahtstelle x0 stetig,
wenn gilt:
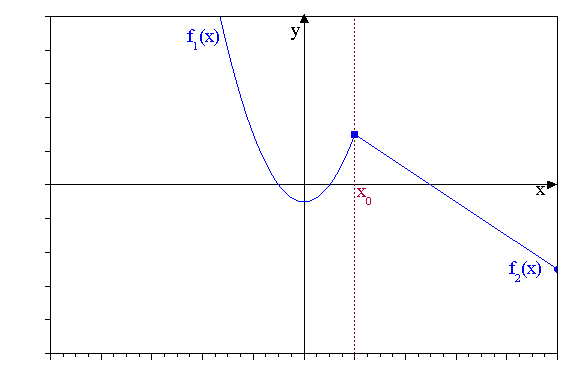
Für den Graphen einer Funktion bedeutet dies, dass er ohne den Zeichenstift
abzusetzen gezeichnet werden kann, d.h. keine „Sprungstelle“ besitzt,
wie im folgenden Beispiel dargestellt:
