Bei Zufallsexperimenten interessieren eigentlich weniger die einzelnen Ergebnisse (z.B. "Bube" oder "Dame"), sondern vielmehr die Zahlenwerte, die diesen Ergebnissen zugeordnet sind (z.B. die Wertigkeiten dieser Karten, oder der Gewinn bei der Ziehung einer Karte). Diese Zuordnung wird als Zufallsgröße X bezeichnet.
Sie ist also eine Funktion, die jedem Ergebnis eines Ergebnisraumes als Definitionsmenge eine reelle Zahl, die Zufallswerte zuordnet.

Bestimmen Sie nun zu folgenden Beispielen die Zufallsgröße X und die Werte der Zufallsgröße.

Beispiel 1:
Eine Münze wird zweimal geworfen. Wie oft kann dabei „Kopf“ erscheinen?

Beispiel 2:
Beim Roulette setzt man z.B. entweder auf rot oder schwarz.
Wenn die Kugel auf der vorausgesagten Farbe liegen bleibt, wird der doppelte Einsatz ausgezahlt,
sonst ist der Einsatz verloren.
Ein Spieler setzt nun 2 € auf rot. Welche Möglichkeiten gibt es für den Gewinn?

Beispiel 3:
In einer Schachtel befinden sich zwei Paar Socken in verschiedenen Farben (ein blaues Paar und ein rotes Paar). Da man nicht in die Schachtel sehen kann und die Socken nicht geordnet sind, wird nun so lange eine Socke gezogen, bis man das rote Paar komplett hat.
Wie viele Ziehungen können nötig sein?

2. Wahrscheinlichkeitsverteilung

Jedem Wert x_i der Zufallsgröße X wird nun eine Wahrscheinlichkeit zugeordnet.
Diese Wahrscheinlichkeit bezeichnet man mit P(X=x_i).
Die Schreibweise "P(X=x_i)" bedeutet die Wahrscheinlichkeit (P), dass die Zufallsgröße (X) einen bestimmten Wert x_i, also einen bestimmten Wert aus den möglichen Zufallswerten annimmt.
Die Funktion P, die jedem Wert x_i der Zufallsgröße X die Wahrscheinlichkeit P(X=x_i) zuordnet, nennt man Wahrscheinlichkeitsverteilung der Zufallsgröße X.

Erstellen Sie nun eine Tabelle der Wahrscheinlichkeitsverteilung der Zufallsgröße folgender Zufallsexperimente.
(Dazu sollen vorher die Elementarereignisse und ihre Wahrscheinlichkeiten bestimmt werden.)

Beispiel 1:
Eine Münze wird 2 mal geworfen.
Die Zufallsgröße X ist die Anzahl der geworfenen Seite "Kopf".

Beispiel 2:
Bei einem Glücksspiel zahlt man 5 € ein und würfelt dann mit drei Würfeln.
Zeigen alle drei Würfel die Zahl sechs, so erhält man 20 €,
zeigen zwei Würfel die Zahl sechs, so erhält man 15 €,
zeigt ein Würfel die Zahl sechs, so erhält man 10 €.
Die Zufallgröße X ist der Reingewinn.

Stabdiagramm und Histogramm

Die Wahrscheinlichkeitsverteilung kann nach dem Erstellen der Wertetabelle mit einem Stabdiagramm oder mit einem Histogramm graphisch dargestellt werden.
Da der Funktionsgraph nur aus Punkten besteht, zeichnet man die Ordinaten der Funktion beim Stabdiagramm als Stäbe und beim Histogramm als Balken.

Stabdiagramm:	Histogramm:

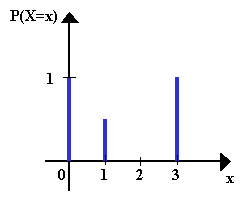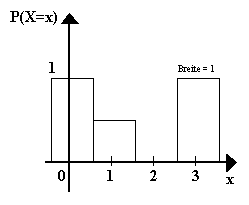Erstellen Sie nun zu den Beispielen jeweils ein Stabdiagramm und Histogramm.

Diagramme zu Beispiel 1:

Diagramme zu Beispiel 2:

3. Erwartungswert

Um einen Durchschnittswert aus n Zahlen x₁ ,....., x_nzu ermitteln, verwendet man folgende Formel:

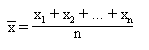
Treten dabei jedoch viele gleiche Werte auf, etwa wie in folgender Liste,
{1; 1; 1; 2; 2; 2; 2; 2; 3; 3; 4; 4; 4; 4; 4; 4; 5; 5; 5; 5}
dann wird niemand die 20 Werte addieren und dann durch 20 teilen, sondern diese Werte gruppieren:
3 mal 1, 5 mal 2, 2 mal 3, 6mal 4 und 4 mal 5. Der Mittelwert würde dann folgendermaßen berechnet werden:

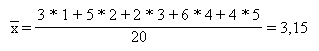
Die dazugehörige Formel würde also lauten:

(Es wurden hier k verschiedene Werte verwendet.
Im Nenner steht die Gesamtzahl n, für die gilt: n = n₁+n₂+...+n_k.)

Die Gleichung für kann man durch Zerlegen in einzelne Brüche in eine neue Formel umformen:

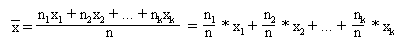
Die nun auftretenden Brüche sind relative Häufigkeiten h₁ ,....., h_k der "Ereignisse" x₁ ,....., x_k:

Somit sieht die Formel für den Mittelwert bei relativen Häufigkeiten folgendermaßen aus:

=

Da die relative Häufigkeit bei sehr vielen Versuchen bei uns stets als Wahrscheinlichkeit interpretiert wird, kann daraus folgende Formel abgeleitet werden:

E(X) steht für den Erwartungswert der Zufallsgröße X.
Der Erwartungswert ist also ein Durchschnittswert aller Werte der Zufallsgröße, der sich bei sehr häufigem Wiederholen des Experimentes ergibt.
Wenn der Verlust bzw. der Gewinn bei Glücksspielen berechnet wird, so werden die Spiele als "fair" bezeichnet, wenn der Erwartungswert bei 0 liegt.

Nun können Sie den Erwartungswert der Beispiele von Nr. 2 Wahrscheinlichkeitsverteilung ausrechnen.

Beispiel 1:

Beispiel 2:

4. Streuung von Zufallsvariablen

Zur Verdeutlichung sind folgende Wahrscheinlichkeitsverteilungen gegeben:

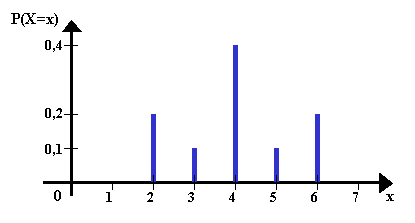
Verteilung 1:

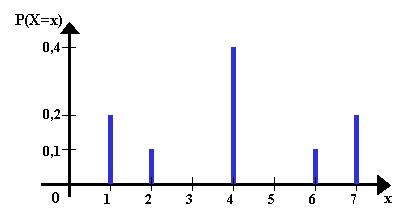
Verteilung 2:

Berechnen Sie nun die Erwartungswerte beider Wahrscheinlichkeitsverteilungen!

Wodurch unterscheiden sich die beiden Wahrscheinlichkeitsverteilungen?

Das Maß für die Streuung der Zufallswerte um den Erwartungswert wird Standardabweichung genannt. Sie gibt also einen mittleren Wert aller Abweichungen vom Erwartungswert an.
Um die Standardabweichung zu berechnen, muss vorher die Varianz ausgerechnet werden.
Dafür gibt es definitionsgemäß folgende Formel:

Aus dieser Formel lässt sich wiederum eine weitere Formel ableiten (auf die Herleitung wird hier verzichtet), mit der es einfacher ist, die Varianz einer Zufallsgröße auszurechnen. Diese wird als Verschiebungsformel bezeichnet.

Da bei der Varianz durch das Quadrieren der Abweichung (x_i – µ) die Einheit (z.B. Euro)verändert wurde (z.B."Quadrat-Euro") , wird nun aus der Varianz die Wurzel gezogen und man erhält die Standardabweichung der Zufallsgröße X, die wieder die gleiche Einheit wie X und E(X) hat:

Nun können Sie auch die Varianzen und die Standardabweichungen der Wahrscheinlichkeitsverteilungen 1 und 2 errechnen!

Beispiel:
Ein Roulette-Spiel besteht aus 37 Zahlen, nämlich der weißen Null, 18 roten und 18 schwarzen Zahlen.
Setzt man nun entweder auf die Farben rot oder schwarz oder auf eine Zahl von 0 bis 37 , so gilt :
- beim Erraten der richtigen Farbe wird der doppelte Einsatz ausgezahlt.
- beim Erraten der richtigen Zahl wird der 36-fache Betrag ausgezahlt.
Berechnen Sie nun die Standardabweichungen der beiden Spielvarianten bei einem Einsatz von 2 €,
wenn die Zufallsgröße X der Gewinn ist !

Wie kann nun die Standardabweichung im Bezug auf das Verlustrisiko bei Glücksspielen interpretiert werden?