1. Geben Sie zu den angegebenen Versuchen eine Wahrscheinlichkeitsverteilung an und erstellen Sie danach ein Histogramm oder ein Stabdiagramm.

   1. Zwei unterscheidbare Würfel werden geworfen. Die Zufallsgröße X ist die Anzahl der erschienenen Augenzahl 1.
      
   2. Eine Münze wird so lange geworfen, bis eine von beiden Seiten zum zweiten Mal erscheint. Die Zufallsgröße X ist die Anzahl der benötigten Würfe.
      

    

2. Bei CD-Playern kommt es darauf an, dass die Drehzahl möglichst konstant bleibt.
   Die Antriebsmotoren zweier Firmen A und B werden getestet. Dabei werden die Abweichungen vom Sollwert in 4 Stufen eingeteilt. Man ermittelt folgende Tabelle:
   
   

   Abweichungsgrad	0	1	2	3
   Firma A	0,70	0,20	0,06	0,04
   Firma B	0,76	0,04	0,20	0

   
   
   1. Berechnen Sie den Erwartungswert des Abweichungsgrades der Firmen und die Standardabweichung.
      
   2. Welche Firma liefert die besseren Antriebsmotoren?
      

    

3. In einer Urne befinden sich 2 schwarze und 3 weiße Kugeln. Man zieht gleichzeitig (= nacheinander ohne zurücklegen) 3 Kugeln.
   Der Einsatz beträgt 2 €. Für jede gezogene schwarze Kugel erhält man 2 € ausbezahlt.
   Die Zufallsgröße X ist der Gewinn / Verlust (= negativer Gewinn) bei der Durchführung eines Spiels.

1. Geben Sie den Ergebnisraum an und bestimmen Sie die Wahrscheinlichkeit der Elementarereignisse
   
2. Ermitteln Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße X und zeichnen Sie ein Histogramm
   
3. Ermitteln Sie rechnerisch den Erwartungswert der Zufallsgröße X
   
4. Ermitteln Sie rechnerisch Varianz und Standardabweichung der Zufallsgröße X
   
5. Wie viel Geld müsste man für eine schwarze Kugel bekommen, damit es ein faires Spiel wird?
   (Der Einsatz soll weiterhin 2 € betragen)
   

 

4. Bei Einwurf von 1 € setzen sich unter einer Sichtscheibe zwei mit Ziffern beschriftete Räder in Bewegung. Jedes Rad lässt immer nur eine Ziffer sichtbar erscheinen. Auf dem linken Rad befinden sich einmal die Ziffer 1, einmal die Ziffer 2 und dreimal die Ziffer 3. Auf dem rechten Rad befinden sich nur die Ziffern 1 und 3. Die Ziffern 1 und 3 treten gleich oft auf.

   Es wird folgender Auszahlungsplan festgelegt:
   Zeigen beide Räder die gleiche Ziffer an, erhält der Spieler 2 € ausbezahlt.
   Zeigen beide Räder zwei Ziffern an, die sich um die Zahl 1 unterscheiden, erhält der Spieler 0,50 € ausbezahlt.
   In den anderen Fällen wird nichts ausbezahlt.
   
   Die Zufallsgröße X ist der Gewinn pro Spiel

   1. Bestimmen Sie die Wahrscheinlichkeitsverteilung für die Zufallsgröße X und erstellen Sie ein Stabdiagramm zu dieser Verteilung
      
   2. Wie groß ist die Wahrscheinlichkeit, dass man beim Spielen verliert?
      
   3. Berechnen Sie den Erwartungswert dieses Spieles. Liegt ein faires Spiel vor?
      
   4. Berechnen Sie, welche Auszahlung erfolgen muss, wenn die Räder gleiche Zahlen anzeigen, damit ein faires Spiel entsteht (die anderen Werte sollen nicht verändert werden).
      

    

5. Bei der Aussaat werden Samenkörner in die Erde gelegt. Nach frühestens drei Tagen Keimzeit zeigen sich die ersten Triebe. Samen, die unter gleichbleibend günstigen Bedingungen nach dem siebten Tag noch nicht gekeimt haben sind erfahrungsgemäß unfruchtbar.
   Von 1000 aufgegangenen Samenkörnern zeigten sich bei 120 der Pflänzchen die ersten Triebe bereits nach drei Tagen, bei weiteren 350 nach vier Tagen, bei 300 nach fünf, bei 170 nach sechs und bei 60 nach sieben Tagen.
   Die Zufallsgröße X gibt die Anzahl der ganzen Tage bis zum Keimtag an. (Keimdauer x).

   1. Erstellen Sie eine Wertetabelle, in der jedem Wert x der Zufallsgröße X seine Wahrscheinlichkeit P(X=x) zugeordnet wird, und zeichnen die dazu ein Histogramm
      
   2. Berechnen Sie die mittlere Keimdauer E(X), und bestimmen Sie die Wahrscheinlichkeit dafür, dass die Werte der Zufallsgröße X um weniger als 20% vom Erwartungswert E(X) abweichen.
      

    

Bei einem Kindergartenfest ist die Hauptattraktion ein in acht gleich große Sektoren unterteiltes Glücksrad. Fünf der Sektoren sind rot, zwei grün und einer blau gefärbt. Zur Rotation gebracht, kommt das Rad nach kurzer Zeit zum Stillstand und eine der Farben erscheint in einem Fenster.
Bei einem Spiel wird das Glücksrad zweimal nacheinander zur Rotation gebracht. Erscheint beide Male der blaue Sektor, so erhält der entsprechende "Spieler" 10 Gummibärchen als Gewinn, bei zwei grünen Sektoren 8 Bärchen, bei zwei roten 3 Bärchen; in allen anderen Fällen wird 1 Bärchen als "Trostpreis" vergeben.
Die Zufallsgröße X gibt die Anzahl der in einem Spiel gewonnenen Gummibärchen an.

1. Bestimmen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße X und zeichnen Sie ein zugehöriges Histogramm.
   
2. Berechnen Sie den Erwartungswert und die Standardabweichung der Zufallsgröße X.
   

 

7. Der Boden eines Badezimmers wird gefliest. Erfahrungsgemäß können auf einer gefliesten Fläche von der Größe dieses Sanitärraums innerhalb des ersten Jahres nach Verlegung der betreffenden Fliesensorte insgesamt höchstens fünf Risse auftreten. Die Zufallsgröße X gibt die Anzahl der Risse in den Fliesen des Badezimmers an, die in diesem Zeitraum entstehen. 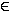Mit geeigneten Werten von a und b (a, b [0;1] ) lässt sich die Wahrscheinlichkeitsverteilung der Zufallsgröße X wie folgt darstellen:
   
   

   x	0	1	2	3	4	5
   P(X=x)	a	0,25	3b	0,1	b	0,05

   
   
   1. Berechnen Sie a und b unter der Voraussetzung, dass die Wahrscheinlichkeit dafür, dass höchstens zwei Risse auftreten, 0,8 beträgt.
      
   2. Berechnen Sie die Wahrscheinlichkeit dafür, dass die Anzahl der Risse innerhalb der einfachen Standardabweichung um den Erwartungswert liegt.
      

    

8. In einer größeren Gebäckschale liegen viele Kekse in den beiden Füllungsvarianten Vanillecreme ( V-Kekse ) und Haselnusscreme ( H-Kekse ). Die Kekse sind mit Schokoladenglasur überzogen, formgleich und somit äußerlich nicht unterscheidbar. Der Schale werden nacheinander drei Kekse zufällig ohne Zurücklegen entnommen. Die Zufallsgröße X gibt die Anzahl der H-Kekse unter den drei entnommenen Keksen an. 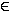Die Wahrscheinlichkeitsverteilung der Zufallsgröße X lässt sich mit Hilfe der Parameter a, b [0; 1] wie folgt darstellen:
   
   

   x	0	1	2	3
   P(X=x)	20a	5b	2b	a

   
   Der Erwartungswert der Zufallsgröße X beträgt µ=1.
   
   
   1. Berechnen Sie die Parameter a und b.
      
   2. Stellen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße X in Form eines Histogramms dar und schraffieren Sie in diesem Histogramm die zu P(X ≤ µ) gehörende Fläche.
      

    

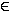9. Beim Druck von Briefmarken können drei Fehlerarten auftreten, nämlich Fehler bei der Zähnung, beim Farbton und bei der Grafik. Die Zufallsgröße X gibt die Anzahl der Fehlerarten an, die bei einer zufällig ausgewählten Briefmarke des Drucks auftreten. Die Wahrscheinlichkeitsverteilung der Zufallsgröße X kann mit Hilfe eines geeigneten Parameters a IR so dargestellt werden:
   
   

   x	0	1	2	3
   P(X = x)	0,4a	0,025a2	0,05	0,05

   
   
   1. Berechnen Sie den Parameter a.
      
   2. Berechnen Sie die Wahrscheinlichkeit dafür, dass der Wert der Zufallsgröße innerhalb der zweifachen Standardabweichung um den Erwartungswert liegt.
      

Zum Arbeitsblatt