Frühjahr 2008
Aufgabengruppe S I S II
Allgemeine Vorbemerkung:
Interpretieren Sie bei den folgenden Aufgaben alle
relativen Häufigkeiten als Wahrscheinlichkeiten.
Für die folgenden Teilaufgaben liegt der feinste Ergebnisraum zugrunde.
relativen Häufigkeiten als Wahrscheinlichkeiten.
| 1.0 | In
einer Jugendherberge werden als Getränke nur Saft (s), Wasser (w) und Cola (c) verkauft. Diese kann man am Automaten (a) oder beim Her- bergsvater Max (m) kaufen. Bei ihm gibt es die Getränke gekühlt (k) oder ungekühlt ( 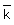 ),
am Automaten nur gekühlt. 60% der Getränke werden am ),
am Automaten nur gekühlt. 60% der Getränke werden amAutomaten gekauft. Der Anteil an Wasser beträgt am Automaten und bei Max jeweils 10%. Cola wird am Automaten zu 60% und bei Max zu 40% gewählt. Wasser geht bei Max nur ungekühlt über die Theke, wobei bei den übrigen Getränken der Anteil der ungekühlten Flaschen jeweils 70% beträgt. Das Zufallsexperiment besteht darin, bei einem beliebig ausgewählten Ge- tränkekauf festzustellen, wo das Getränk gekauft wird, welches Getränk gekauft wird, und ob es gekühlt oder ungekühlt ist. |
| 1.1 | Bestimmen
Sie mit Hilfe eines Baumdiagramms die Wahrscheinlichkeiten aller 8 Elementarereignisse dieses Zufallsexperiments. (6 BE) |
| 1.2 | Geben
Sie zum Zufallsexperiment aus Teilaufgabe 1.0 zwei verschiedene Ergebnisräume an, die sich vom feinsten Ergebnisraum unterscheiden. (2 BE) |
Für die folgenden Teilaufgaben liegt der feinste Ergebnisraum zugrunde.
| 1.3 | Geben
Sie das Ereignis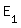 :
„Es wird Saft oder ein ungekühltes Getränk gekauft“ :
„Es wird Saft oder ein ungekühltes Getränk gekauft“in der aufzählenden Mengenschreibweise an und bestimmen Sie die Wahrscheinlichkeit P( 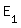 ). ).
(2 BE) |
| 1.4 | Folgende
Ereignisse sind vorgegeben: A: „Ein Getränk wird am Automaten gekauft.“ S: „Es wird eine Flasche Saft gekauft.“ K: „Das gekaufte Getränk ist gekühlt.“ Bestimmen Sie die Wahrscheinlichkeiten 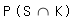 sowie
sowie 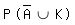 . .
(4 BE) |
| 2 | Es
sind 50 Personen in der Jugendherberge untergebracht. Zum Frühstück gibt es Tee (T) und Orangensaft (O). 40 Personen trinken Tee, 25 Oran- gensaft und 5 Personen trinken nichts zum Frühstück. Untersuchen Sie zB. mit Hilfe einer Vierfeldertafel, ob die Wahl von Orangensaft und Tee stochastisch unabhängig ist. (5 BE) |
| 3.0 | Die
Zufallsgröße X gibt die Anzahl der Tassen Tee an, die ein Gast bei einem Frühstück trinkt. Es ergibt sich folgende Verteilung:
|
||||||||||||||||
| 3.1 | Erstellen
Sie für die Zufallsgröße X die Wahrscheinlichkeitsverteilung und stellen Sie diese geeignet graphisch dar. Berechnen Sie, mit wie viel Tassen Tee der Herbergsvater im Durch- schnitt pro Gast rechnen kann. (4 BE) |
||||||||||||||||
| 3.2 | Berechen
Sie wie viele Tassen Tee Max pro Gast mindestens bereitstel- len muss, wenn die Wahrscheinlichkeit dafür, dass der Tee ausreicht, mehr als 90% betragen soll. (3 BE) |
| 4.0 | Zum
Mittagessen wählen erfahrungsgemäß 3% der Gäste ein vegetari- sches Gericht. |
| 4.1 | Bestimmen
Sie die Wahrscheinlichkeiten folgender Ereignisse: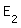 : „Von 50 Gästen wählen mehr als 3 das
vegetarische Gericht.“ : „Von 50 Gästen wählen mehr als 3 das
vegetarische Gericht.“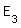 : „Die Zahl der vegetarischen Essen bei 100
Gästen liegt innerhalb der : „Die Zahl der vegetarischen Essen bei 100
Gästen liegt innerhalb der einfachen Standardabweichung um den Erwartungswert.“ 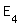 : „Von 100 Gästen essen 99 nicht das
vegetarische Gericht.“ : „Von 100 Gästen essen 99 nicht das
vegetarische Gericht.“
(8 BE) |
| 4.2 | Aus
aktuellen Beobachtungen schließt der Herbergsvater, dass der Anteil der vegetarischen Gerichte zugenommen hat (Gegenhypothese). Um sei- nen Eindruck zu untermauern, führt er einen Test an 200 zufällig ausge- wählten Essensbestellungen durch. Geben Sie für diesen Test die Testgröße sowie die Nullhypothese an und bestimmen Sie auf dem 5%-Niveau den maximalen Ablehnungsbereich der Nullhypothese. Ermitteln Sie für diesen Fall auch die Wahrscheinlich- keit des Fehlers 1. Art. (6 BE) |
