Seminararbeit von Jessica Klein, Oktober 2001
Nachbearbeitung: OStR Starfinger
Inhaltsverzeichnis
- Aufgaben aus dem Bereich der Analysis und der allgemeinen Algebra
- Aufgaben aus dem Bereich der Wirtschaft
- Aufgaben aus dem Bereich Geometrie und Technik
Aufgaben aus dem Bereich der Analysis und der allgemeinen Algebra
- Gegeben ist eine Funktion f mit f(x) = –x2+4. Der Graph schließt mit der x–Achse eine Fläche ein.
- Beschreiben Sie dieser Fläche ein achsenparalleles Rechteck mit möglichst großem Inhalt ein.

- Beschreiben Sie der Fläche ein zur y–Achse symmetrisches gleich- schenkliges Dreieck mit möglichst großem Inhalt ein, dessen Spitze im Punkt N(0;0) liegt.

- Der Graph der Funktion f mit f (x) = (x2 – 4)2 schließt mit der x–Achse eine Fläche ein. Dieser Fläche kann man Dreiecke einbeschreiben, die gleichschenklig und symmetrisch zur y–Achse sind und deren Spitze im Punkt N(0;0) liegt. Lässt man diese Dreiecke um die y–Achse rotieren, entstehen Kegel.
Welcher dieser Kegel hat das größte Volumen? 
- In die Figur aus den Graphen der zwei Funktionen f1(x) = –x2 +1
und f2(x) = 4x2 –10 können Rechtecke mit achsenparallelen Seiten einbeschrieben werden. Welches der möglichen Rechtecke hat den maximalen Inhalt?

- Die Zahl 18 soll in zwei Summanden zerlegt werden. Berechnen Sie diese so, dass
- ihr Produkt maximal wird.

- die Summe ihrer Quadrate minimal wird.

Zerlegen Sie die Zahl 10 in zwei Summanden. Das Produkt aus der 3. Potenz des ersten Summanden und der 2. Potenz des zweiten Summanden soll einen maximalen Wert annehmen. Berechnen Sie die beiden Summanden, sowie den Maximalwert des beschriebenen Produkts. 
Aufgaben aus dem Bereich der Wirtschaft
- Ein Behälter soll die Form einer quadratischen Säule erhalten.
Das Volumen der Säule soll 200 dm betragen. 1 dm
betragen. 1 dm des Materials für die Stand- und Deckfläche kostet 4
des Materials für die Stand- und Deckfläche kostet 4 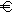 , 1 dm
, 1 dm des Materials für die Seitenfläche kostet 5
des Materials für die Seitenfläche kostet 5 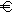 . Welcher der möglichen Behälter verursacht die geringsten Materialkosten?
. Welcher der möglichen Behälter verursacht die geringsten Materialkosten? 
- Ein Supermarkt verkauft pro Woche 750 Tafeln Schokolade zu 1,00
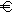 pro Tafel. Der Geschäftsführer rechnet, dass jeder Cent Preissenkung die Verkäufe um 50 Tafeln erhöht. Die Kosten betragen 0,75
pro Tafel. Der Geschäftsführer rechnet, dass jeder Cent Preissenkung die Verkäufe um 50 Tafeln erhöht. Die Kosten betragen 0,75 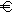 pro Tafel.
pro Tafel.
Um wieviel Cents muss der Preis gesenkt werden, damit der Gewinn maximal wird? 
Aufgaben aus dem Bereich Geometrie und Technik
- Bearbeiten Sie folgende Problemstellungen:
- Welche oben offene Schachtel in der Form einer quadratischen Säule hat bei gegebenem Oberflächeninhalt 3 dm
 ein möglichst großes Fassungsvermögen?
ein möglichst großes Fassungsvermögen? 
- Lösen Sie Aufgabe a., falls die Schachtel anstatt nach oben nach vorn geöffnet ist. In welchem Verhältnis stehen jetzt Höhe und Breite der quadratischen Säule? Ergibt sich ein größeres Volumen?

- Aus einem rechteckigen Stück Pappe mit den Seitenlängen 40 cm und 25 cm soll man einen Kasten ohne Deckel herstellen, indem man an jeder Ecke ein Quadrat ausschneidet und die entstehenden Seitenflächen nach oben biegt. Der Kasten soll ein möglichst großes Volumen haben.


-
Der Querschnitt eines Kanals ist ein Rechteck mit aufgesetztem Halbkreis. Wählen Sie die Maße dieses Rechtecks so, dass bei gegebenem Umfang U des Querschnitts sein Inhalt möglichst groß wird.

- Einem geraden Kreiskegel soll ein zweiter Kegel mit möglichst großem Volumen so einbeschrieben werden, dass die Spitze des zweiten Kegels im Mittelpunkt des Grundkreises des ersten Kegels liegt.

- Ein Dachboden hat als Querschnittsfläche ein gleichschenkliges Dreieck mit einer Höhe von 4,8 m und einer Breite von 8 m. In ihm soll ein möglichst großes quaderförmiges Zimmer eingerichtet werden.

- Welche quadratische Säule mit gegebenem Volumen hat die kürzeste Körperdiagonale?
Beachten und begründen Sie: Mit einer Größe hat auch ihr Quadrat an derselben Stelle ein Extremum. 
- Welche gerade quadratische Pyramide mit gegebenem Volumen hat die kürzeste Seitenkante?

- Welcher einer Kugel einbeschriebene gerade Kreiskegel hat die größte Mantelfläche?

- Lösen Sie die beiden folgenden Aufgaben:
- Einer Pyramide mit quadratischer Grundfläche ist eine quadratische Säule mit maximalem Volumen einzubeschreiben.

- Einem Kegel ist eine quadratische Säule mit maximalem Volumen einzubeschreiben.

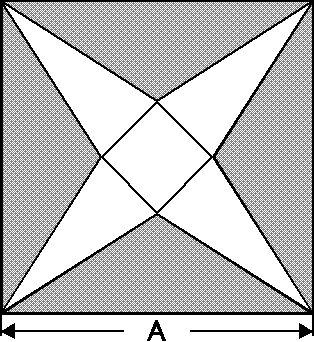
- Gegeben sei ein Quadrat mit der Seitenlänge A. Schneidet man die grauen gleichschenkligen Dreiecke heraus, entsteht das Netz einer geraden Pyramide mit quadratischer Grundfläche.
Welche dieser Pyramiden hat das maximale Volumen? 
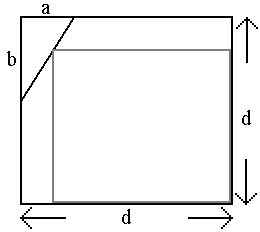
- Aus einer quadratischen Glasscheibe mit der Seitenlänge d = 1m ist ein Eckstück herausgebrochen, das die Form eines rechtwinkligen Dreiecks mit den Katheten a und b besitzt.
Um die zerbrochene Scheibe optimal weiternutzen zu können, wird aus ihr, wie in der Skizze dargestellt, eine möglichst große rechteckige Scheibe heraus-geschnitten.
Wie sind die Maße dieser Scheibe zu wählen, wenn
- a = 0,4m und b = 0,5m;

- a = 0,3m und b = 0,6m?

 betragen. 1 dm
betragen. 1 dm des Materials für die Stand- und Deckfläche kostet 4
des Materials für die Stand- und Deckfläche kostet 4 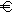 , 1 dm
, 1 dm des Materials für die Seitenfläche kostet 5
des Materials für die Seitenfläche kostet 5 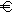 . Welcher der möglichen Behälter verursacht die geringsten Materialkosten?
. Welcher der möglichen Behälter verursacht die geringsten Materialkosten?  pro Tafel. Der Geschäftsführer rechnet, dass jeder Cent Preissenkung die Verkäufe um 50 Tafeln erhöht. Die Kosten betragen 0,75
pro Tafel. Der Geschäftsführer rechnet, dass jeder Cent Preissenkung die Verkäufe um 50 Tafeln erhöht. Die Kosten betragen 0,75  pro Tafel.
pro Tafel. ein möglichst großes Fassungsvermögen?
ein möglichst großes Fassungsvermögen? 

