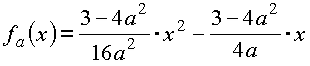Arbeitsblatt Extremwertaufgaben
Seminararbeit von Jessica Klein, Oktober 2001
Inhaltsverzeichnis
- Was versteht man unter Extremwertaufgaben?
- Vorgehensweise bei Extremwertaufgaben
- In welchen Bereichen kommen Extremwertaufgaben vor?
- Arbeitsaufgaben aus verschiedenen Bereichen
4.1 Sportplatz - Flächeninhalt
4.2 Strahlensatz
4.3 Funktionenschar
4.4 Pythagoras
Arbeitsblatt zu Extremwertaufgaben
1. Was versteht man unter Extremwertaufgaben?
Bei Extremwertaufgaben werden die Extrema einer Funktion unter einer oder mehreren Nebenbedingungen berechnet. Die Funktion und die Nebenbedingungen werden durch das vorliegende Problem gegeben. Die Extremwerte müssen häufig mit Hilfe der Differentialrechnung ermittelt werden (relative Extrema). Allerdings können auch Randextrema oder globale Extrema als Lösung in Frage kommen, wenn diese größer als die relativen Extrema sind.
Die Extremwertaufgaben eignen sich als anschauliche Anwendung der Differentialrechnung.
2. Vorgehensweise bei Extremwertaufgaben
Die folgenden Schritte stellen keinen allgemein gültigen Lösungsweg dar, aber sie sollen eine Hilfestellung bei der Lösung von Extremwertaufgaben sein. Die einzelnen Schritte sind zunächst vielleicht etwas abstrakt, werden aber in den unten folgenden Beispielen aufgegriffen und dadurch hoffentlich klarer.
- Schritt - Analyse der Fragestellung
- Was ist gegeben? (Falls möglich Skizze anfertigen!)
- Welche Nebenbedingungen können aus den gegebenen Angaben aufgestellt werden?
- Was ist gesucht?
- Wie lautet die Extremalbedingung?
- Schritt - Aufstellen der Zielfunktion des Problems unter Berücksichtigung der vorhandenen Nebenbedingungen.
- Schritt - Bestimmung der Definitionsmenge des Problems
- Schritt - Berechnung der lokalen Extrema der Zielfunktion
- Schritt - Vergleich der lokalen Extrema mit den Funktionswerten der Zielfunktion an den Rändern des Definitionsbereichs
- Schritt - Berechnung des globalen Extremums der Zielfunktion und Ausformulierung des Ergebnisses
3. In welchen Bereichen kommen Extremwertaufgaben vor?
In Bereichen wie in der Geometrie, in der Algebra, in der Technik, sowie in der Wirtschaft kommen Extremwertaufgaben vor. Dazu sind Kenntnisse der entsprechenden Formeln und Begriffe des Aufgabengebietes notwendig.
Von den geometrischen Formeln sind neben denen für den Umfang, Flächeninhalt und Volumen verschiedener Körper auch der Strahlensatz sowie der Satz von Pythagoras besonders wichtig. Diese Formeln und deren Anwendung werden für die Berechnung vorausgesetzt. (Literatur zur Wiederholung finden Sie: Stoff der 9. u. 10. Klasse an Gymnasien)
4. Arbeitsaufgaben aus verschiedenen Bereichen
Die folgenden Aufgaben behandeln die Themen Flächeninhalt, Strahlensatz, Pythagoras und ein Beispiel aus der Analysis mit einer Funktionenschar.
Zum Einstieg werden die einzelnen Problemstellungen ausführlich anhand der oben angebenen Schritte 1-6 gelöst.
Bei allen Aufgaben ist es wichtig, dass man die benötigten Formeln erkennt und richtig anwenden kann, um gezielt auf die richtige Lösung zu kommen.
Weitere Aufgaben, die zum Arbeiten anregen sollen, finden Sie auf dem
Übungsblatt.
4.1 Aufgabe Sportplatz (siehe auch das dazugehörige Applet)
Eine 400m lange Laufbahn besteht aus zwei parallelen Strecken mit der Länge l und zwei angesetzten Halbkreisen mit dem Radius r. Wie groß müssen l und r gewählt werden, wenn die Rechtecksfläche, das Spielfeld, möglichst groß werden soll?
Schritt 1 - Analyse der Fragestellung
Wir zeichnen uns zunächst eine Skizze des Sportplatzes und überlegen uns, welche Nebenbedingungen sich daraus ergeben.
Skizze
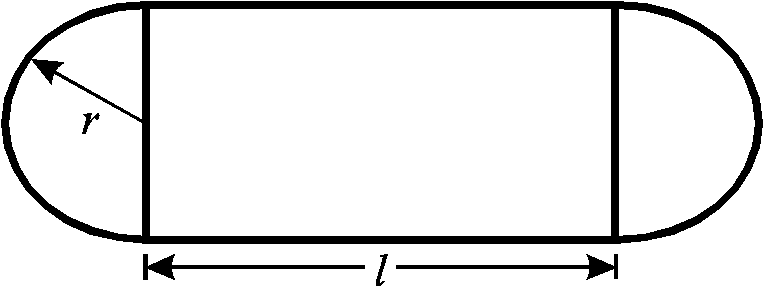
Zuerst fragt man sich, was gegeben und was gesucht ist.
Gegeben ist die Länge l und der Radius r.
Welche Nebenbedingung gilt für l und r? 
Von welcher Größe soll der Extremwert bestimmt werden? (Extremalbedingung)

Schritt 2 - Wie kann man das in einer Funktion ausdrücken? (Zielfunktion) 
Schritt 3 - Welche Definitionsmenge hat die Funktion A(r)? 
Wie kann man sich das mathematische Intervall anhand der Aufgabe vorstellen? 
Schritt 4 - Jetzt muss man das lokale/relative Maximum von A(r) bestimmen.
Wie lauten die lokalen Extrema der Zielfunktion? 
Nun muss man prüfen, ob es sich bei dem berechneten Extremum tatsächlich um ein Maximum handelt. 
Schritt 5 - Vergleich des lokalen Maximums mit den Funktionswerten am Rand von ID
Das berechnete Maximum ist nur dann ein globales Maximum, wenn alle Funktionswerte an den Intervallgrenzen kleiner sind als 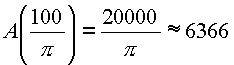
Stimmt dies? 
Schritt 6 - Berechnen Sie nun den Funktionswert am globalen Maximum und formulieren Sie eine Antwort. 
4.2 Strahlensatz und gleichseitiges Dreieck
Einem gleichseitigen Dreieck der Seitenlänge a soll wie in der Skizze ein Rechteck so einbeschrieben werden, dass dessen Flächeninhalt A extremal wird.
Skizze
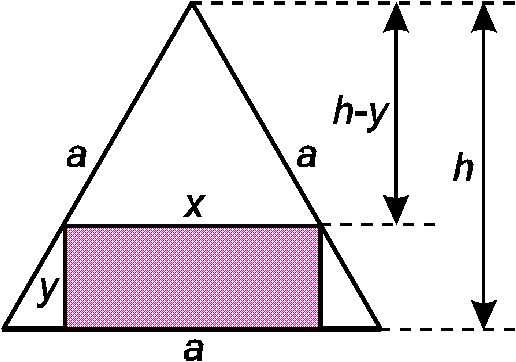
Schritt 1 - Was ist gegeben und gesucht?
Anhand der Skizze kann man erkennen, dass für die Länge und für die Breite andere Variablen eingeführt wurden, die es beim Rechnen leichter machen.
Überlegen Sie sich, wie Sie am besten vorgehen.
Wie lautet der Flächeninhalt des Rechtecks allgemein?
Welcher Satz aus der Geometrie hilft bei der Aufstellung der Nebenbedingung weiter?

Nachdem Sie sich mit dem Strahlensatz auseinandergesetzt haben, überlegen Sie sich, wie Sie ihn bei der Aufgabe anwenden. Achten Sie genau auf die einzelnen Strecken, die Sie in der Skizze sehen.
Wie lautet also die Strahlensatzformel? 
Schritt 2 - Aufstellen der Zielfunktion
Jetzt hat man einen Term mit x, den man in 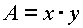 einsetzen kann.
einsetzen kann.
Wie lautet dann die endgültige Ausgangsformel, d.h. die Zielfunktion? 
Schritt 3 - Bestimmung der Definitionsmenge
Wie lautet die Definitionsmenge zu der Funktion? 
Schritt 4 - Berechnung der lokalen Extrema 
Schritt 5 - Lokales Extremum und globales Extremum
Die 2. Ableitung bilden und ihr Vorzeichen an der Stelle 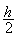 untersuchen. Wie gehen Sie vor?
untersuchen. Wie gehen Sie vor? 
Sie müssen jetzt den zugehörigen x-Wert aus 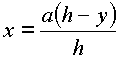 berechnen.
berechnen.  Nun müssen Sie wieder überprüfen, ob es sich um ein globales Extremum handelt.
Nun müssen Sie wieder überprüfen, ob es sich um ein globales Extremum handelt.
Wie lauten die Randwerte (Funktionswerte an den Grenzen der Definitionsmenge)? 
Schritt 6
Jetzt wird der größtmögliche Flächeninhalt berechnet und das Ergebnis zusammengefasst.
Welche Fläche hat das größte Rechteck? 
Bei jeder Textaufgabe ist es wichtig das Ergebnis zu formulieren.
Nehmen Sie sich Zeit und gehen Sie die letzten Schritte noch einmal genau durch und formulieren Sie anschließend den Antwortsatz. 
4.3 Funktionenschar
Gegeben ist die Funktionenschar
mit der Definitionsmenge ID=IR und der Konstante 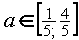 . Die Graphen dieser Schar sind nach oben geöffnete Parabeln. Die Parabeln schneiden die x-Achse in A(0/0) und B(4a/0) und haben den Scheitel
. Die Graphen dieser Schar sind nach oben geöffnete Parabeln. Die Parabeln schneiden die x-Achse in A(0/0) und B(4a/0) und haben den Scheitel 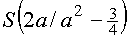 .
.
Skizze:
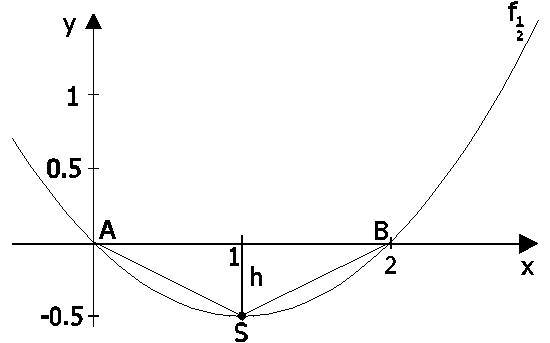
Verbindet man die Punkte A,B und S miteinander, so erhält man ein Dreieck.
Wie ist a zu wählen, damit dieses Dreieck den größtmöglichen Flächeninhalt besitzt?
Schritt 1 - Was ist gegeben und was ist gesucht? 
Schritt 2 - Aufstellen der Zielfunktion
Wie lautet allgemein die Formel des Flächeninhalts eines Dreiecks? 
Stellen Sie bitte eine Funktion mit zwei Variablen auf und erklären Sie dies.

Jetzt haben Sie kennengelernt, wie man den Flächeninhalt des Dreiecks ausrechnen kann. Versuchen Sie den Zusammenhang dieser Formel mit der Skizze in eine Ausgangsformel umzuwandeln. Sie überlegen sich zuerst, wie Sie die Grundseite g des Dreiecks richtig (s. Skizze) einordnen. 
Wie man auf der Skizze erkennen kann, ist die Höhe h auf der Grundseite das Lot vom Scheitel S auf die x-Achse. Jetzt untersucht man die Lage des Scheitels in Abhängigkeit des Parameters a. Wie gehen Sie am besten vor? 
Wie lautet damit der Flächeninhalt? 
Schritt 3 - Geben Sie ID der Zielfunktions an! 
Schritt 4 - Berechnung der lokalen Extrema
Wie lautet die 1. und 2. Ableitung der Funktion? 
Wie erhält man die Extrema? 
Was können Sie aus der Lösung erkennen?
Gehen Sie die ersten Schritte noch einmal durch und überlegen Sie sich genau, was als nächster Schritt für uns von Bedeutung ist. 
Wir untersuchen die Art des Extremums. Wie gehen Sie vor? 
Schritt 5 - Relatives = absolutes Extremum?

Schritt 6 - Wie formulieren Sie den Antwortsatz? 
4.4 Arbeitsaufgabe: Pythagoras
Einer Halbkugel ist ein Zylinder mit möglichst großem Volumen einzubeschreiben.
Skizze
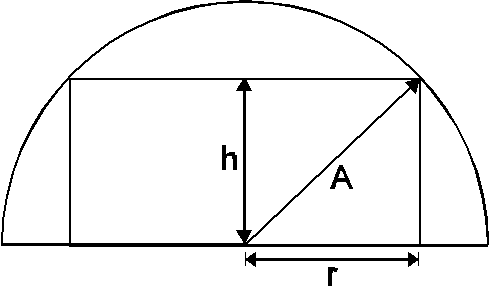
Unter den Voraussetzungen der vorigen Aufgaben versuchen Sie jetzt diese Aufgabe selbständig zu lösen. Achten Sie darauf, was gesucht ist und bilden Sie die dazugehörige Zielfunktion, um das maximale Zylindervolumen zu bestimmen. 
Link zum Übungsblatt zu Extremwertaufgaben
Jessica Klein, Oktober 2001

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

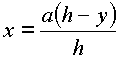 berechnen.
berechnen.