Arbeitsblatt Exponentialfunktion
OStR Starfinger
a) Einführung
Unter der „allgemeinen Exponentialfunktion“ versteht man eine Funktion der Form
f: x | ax, x
ax, x  IR.
1. Für welche a
IR.
1. Für welche a  IR ist die allgemeine Exponentialfunktion definiert? Geben Sie
ein Gegenbeispiel an!
IR ist die allgemeine Exponentialfunktion definiert? Geben Sie
ein Gegenbeispiel an!  2. Stellen Sie für a = 2 und für a = 3 Wertetabellen der zugehörigen Exponential-
funktionen auf, und zeichnen Sie die Grafen! Beschreiben Sie exakt den Verlauf
beider Grafen, und zwar auch im Verhältnis zueinander!
2. Stellen Sie für a = 2 und für a = 3 Wertetabellen der zugehörigen Exponential-
funktionen auf, und zeichnen Sie die Grafen! Beschreiben Sie exakt den Verlauf
beider Grafen, und zwar auch im Verhältnis zueinander!  b) Die Zahl „e“
Die folgende kleine Bildersequenz zeigt eine interessante Beziehung zwischen den
Grafen ausgewählter Exponentialfunktionen und denen ihrer Ableitungsfunktionen
auf.
Schauen Sie sich nun diese Bildersequenz an!
3. Welche Beziehung zwischen den Grafen der Exponentialfunktionen und denen
ihrer Ableitungsfunktionen fällt in der Bildersequenz auf?
b) Die Zahl „e“
Die folgende kleine Bildersequenz zeigt eine interessante Beziehung zwischen den
Grafen ausgewählter Exponentialfunktionen und denen ihrer Ableitungsfunktionen
auf.
Schauen Sie sich nun diese Bildersequenz an!
3. Welche Beziehung zwischen den Grafen der Exponentialfunktionen und denen
ihrer Ableitungsfunktionen fällt in der Bildersequenz auf?  Sie erkennen, dass es eine Zahl e ≈ 2,75 geben muss, so dass gilt:
Sie erkennen, dass es eine Zahl e ≈ 2,75 geben muss, so dass gilt:
Wir versuchen nun, diese „Eulersche Konstante“ e genauer zu ermitteln.
4.1 Stellen Sie für die Funktion f: x | ex den Differenzenquotienten (d. h. die
Sekantensteigungsformel) auf und klammern Sie e
ex den Differenzenquotienten (d. h. die
Sekantensteigungsformel) auf und klammern Sie e aus!
aus!  4.2 Gegen welchen Wert strebt für h
4.2 Gegen welchen Wert strebt für h  0 der Bruch
0 der Bruch 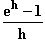 ?
?  4.3 Welcher Grenzwert für die Zahl e ergibt sich aus dem Grenzwert von 4.2 ?
(Tipp: h ≈ 0 setzen und Resultat von Aufgabe 4.2 nach e auflösen!)
4.3 Welcher Grenzwert für die Zahl e ergibt sich aus dem Grenzwert von 4.2 ?
(Tipp: h ≈ 0 setzen und Resultat von Aufgabe 4.2 nach e auflösen!)  Da die Zahlenfolge
Da die Zahlenfolge 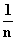 (n = 1; 2; 3; . . .) gegen 0 strebt, kann im Resultat von
Aufgabe 4.3 h durch
(n = 1; 2; 3; . . .) gegen 0 strebt, kann im Resultat von
Aufgabe 4.3 h durch 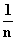 ersetzt werden. Damit ergibt sich für die Zahl e die
berühmte Näherung:
ersetzt werden. Damit ergibt sich für die Zahl e die
berühmte Näherung:
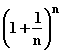  e (n = 1; 2; 3; . . .) e (n = 1; 2; 3; . . .) |
4.4 Setzen Sie nun der Reihe nach in diese Formel n = 1; 2; 4; 8; 16; . . . ein, und
ermitteln Sie auf diese Weise die Zahl e auf 3 Dezimalen genau!  c) Die Umkehrfunktionen der Exponentialfunktionen
5. Gegeben ist die Funktion f: x |
c) Die Umkehrfunktionen der Exponentialfunktionen
5. Gegeben ist die Funktion f: x | 2x – 3.
5.1 Bestimmen Sie die Gleichung der Funktion g mit der Eigenschaft g(f(x)) = x.
2x – 3.
5.1 Bestimmen Sie die Gleichung der Funktion g mit der Eigenschaft g(f(x)) = x.
 5.2 Zeichnen Sie die Grafen der beiden Funktionen f und g in das selbe Koordi-
natensystem! In welcher Beziehung stehen die Grafen zueinander?
5.2 Zeichnen Sie die Grafen der beiden Funktionen f und g in das selbe Koordi-
natensystem! In welcher Beziehung stehen die Grafen zueinander?  6.1 Mit welcher Eigenschaft ist eine Funktion garantiert umkehrbar?
6.1 Mit welcher Eigenschaft ist eine Funktion garantiert umkehrbar?  6.2 Warum sind alle Exponentialfunktionen der Form f: x |
6.2 Warum sind alle Exponentialfunktionen der Form f: x | ax, x
ax, x IR
IR 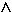 a
a IR+
umkehrbar?
IR+
umkehrbar?  7. Gegeben ist die Exponentialfunktion f: x |
7. Gegeben ist die Exponentialfunktion f: x | 10x, x
10x, x  IR mit ihrer Umkehr-
funktion g.
7.1 Erstellen Sie eine Wertetabelle für die Umkehrfunktion g. Wählen Sie dabei
nur x-Werte, die Zehnerpotenzen darstellen.
7.2 Beschreiben Sie die Wirkung der Funktion g in Worten.
IR mit ihrer Umkehr-
funktion g.
7.1 Erstellen Sie eine Wertetabelle für die Umkehrfunktion g. Wählen Sie dabei
nur x-Werte, die Zehnerpotenzen darstellen.
7.2 Beschreiben Sie die Wirkung der Funktion g in Worten.  Die Funktion g(x) von Aufgabe 7 heißt „Logarithmus von x zur Basis 10“ oder
kurz: „Zehnerlogarithmus von x“.
Schreibweise: g(x) = log10x. Wegen der Beliebtheit des Zehnerlogarithmus
lässt man die 10 oft einfach weg und schreibt nur „log x“ oder sogar nur „lg x“.
7.3 Probieren Sie den Zehnerlogarithmus auf Ihrem Taschenrechner aus!
Allgemein besitzt die Exponentialfunktion f(x) = ax, a
Die Funktion g(x) von Aufgabe 7 heißt „Logarithmus von x zur Basis 10“ oder
kurz: „Zehnerlogarithmus von x“.
Schreibweise: g(x) = log10x. Wegen der Beliebtheit des Zehnerlogarithmus
lässt man die 10 oft einfach weg und schreibt nur „log x“ oder sogar nur „lg x“.
7.3 Probieren Sie den Zehnerlogarithmus auf Ihrem Taschenrechner aus!
Allgemein besitzt die Exponentialfunktion f(x) = ax, a IR+, die Umkehrfunktion
g(x) = logax.
Es gilt also:
IR+, die Umkehrfunktion
g(x) = logax.
Es gilt also:
| loga(ax) = x und alogax = x |
8.1 Welche max. Definitionsmengen besitzen die Logarithmusfunktionen?  8.2 Welche gemeinsame Nullstelle besitzen die Logarithmusfunktionen?
8.2 Welche gemeinsame Nullstelle besitzen die Logarithmusfunktionen?  Die Umkehrfunktion g(x) der Funktion f(x) = ex heißt „natürlicher Logarithmus
von x“, kurz: ln x.
Im Folgenden genügt es, die Exponentialfunktion f: x |
Die Umkehrfunktion g(x) der Funktion f(x) = ex heißt „natürlicher Logarithmus
von x“, kurz: ln x.
Im Folgenden genügt es, die Exponentialfunktion f: x | ex und ihre Derivate zu
untersuchen, da sich alle anderen Exponentialfunktionen auf diese eine zurück-
führen lassen:
ex und ihre Derivate zu
untersuchen, da sich alle anderen Exponentialfunktionen auf diese eine zurück-
führen lassen:
| ax = (eln a)x = e(ln a)·x |
Bearbeiten Sie nun vom Übungsblatt die Aufgaben 1 und 2 !
d) Nullstellenbestimmung
Der natürliche Logarithmus als Umkehrfunktion der e-Funktion ist immer dann
wichtig, wenn es darum geht, die Funktionsvariable x aus dem Exponenten
„herunterzuholen“. Das ist stets bei der Nullstellenbestimmung einer Exponential-
funktion der Fall. Hier ergibt sich nämlich immer eine Exponentialgleichung der
Form eg(x) = c mit c  IR.
Wenn c positiv ist, lässt sich auf beiden Seiten der natürliche Logarithmus
anwenden, und man erhält: g(x) = ln c. Die Lösungen dieser Gleichung sind dann
die Nullstellen der ursprünglichen Exponentialfunktion.
9. Bestimmen Sie die Nullstellen der folgenden Funktionen:
9.1 f: x |
IR.
Wenn c positiv ist, lässt sich auf beiden Seiten der natürliche Logarithmus
anwenden, und man erhält: g(x) = ln c. Die Lösungen dieser Gleichung sind dann
die Nullstellen der ursprünglichen Exponentialfunktion.
9. Bestimmen Sie die Nullstellen der folgenden Funktionen:
9.1 f: x | ex – 1
ex – 1  9.2 f: x |
9.2 f: x | ex2+1 – e2
ex2+1 – e2  9.3 f: x |
9.3 f: x | e2x – ex – 2
e2x – ex – 2  9.4 f: x |
9.4 f: x |
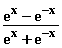
 Bearbeiten Sie nun vom Übungsblatt die Aufgaben 3 und 4 !
e) Knifflige Grenzwerte
Bei der Grenzwertbestimmung von Funktionen, die die e-Funktion enthalten,
können knifflige Fälle auftreten, die zu Ausdrücken der Form
Bearbeiten Sie nun vom Übungsblatt die Aufgaben 3 und 4 !
e) Knifflige Grenzwerte
Bei der Grenzwertbestimmung von Funktionen, die die e-Funktion enthalten,
können knifflige Fälle auftreten, die zu Ausdrücken der Form 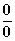 oder
oder 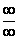 führen.
10.1 Überzeugen Sie sich davon, dass die Funktion f: x |
führen.
10.1 Überzeugen Sie sich davon, dass die Funktion f: x |
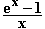 für x
für x  0
einen solchen kniffligen Grenzwert besitzt!
10.2 Ermitteln Sie diesen Grenzwert mit Hilfe des Taschenrechners!
Mit dem Taschenrechner ergibt sich:
0
einen solchen kniffligen Grenzwert besitzt!
10.2 Ermitteln Sie diesen Grenzwert mit Hilfe des Taschenrechners!
Mit dem Taschenrechner ergibt sich: 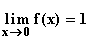 .
Dass wir hier aber nicht auf die empirische Grenzwertermittlung mit dem Taschen-
rechner angewiesen sind, verdanken wir der „Regel von de L'Hospital“.
Sie besagt:
.
Dass wir hier aber nicht auf die empirische Grenzwertermittlung mit dem Taschen-
rechner angewiesen sind, verdanken wir der „Regel von de L'Hospital“.
Sie besagt:
Sind zwei Funktionen f1 und f2 differenzierbar, und gilt f1(x0) = f2(x0) = 0, so gilt:
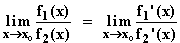 |
Der Beweis dieser Regel ist ganz einfach.
11.1 Testen Sie diese Regel an der rationalen Funktion f: x |
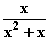 ,
indem Sie den Grenzwert von f an der hebbaren Definitionslücke x = 0
einmal durch Kürzen und zum andern durch Anwendung der Regel von
de L'Hospital bestimmen!
,
indem Sie den Grenzwert von f an der hebbaren Definitionslücke x = 0
einmal durch Kürzen und zum andern durch Anwendung der Regel von
de L'Hospital bestimmen!  11.2 Bestimmen Sie nun den Grenzwert der Funktion f von Aufgabe 10 für x
11.2 Bestimmen Sie nun den Grenzwert der Funktion f von Aufgabe 10 für x 0
mit Hilfe der Regel von de L'Hospital!
0
mit Hilfe der Regel von de L'Hospital!  Die Regel von de L'Hospital erlaubt mit einigen Umformungen drei Schluss-
folgerungen:
12. Wohin streben die Werte der Funktion f von Aufgabe 10, wenn x gegen
+∞ bzw. gegen –∞ strebt?
Die Regel von de L'Hospital erlaubt mit einigen Umformungen drei Schluss-
folgerungen:
12. Wohin streben die Werte der Funktion f von Aufgabe 10, wenn x gegen
+∞ bzw. gegen –∞ strebt?  13. Gegeben ist die Funktion f: x |
13. Gegeben ist die Funktion f: x |
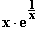 mit ID
mit ID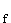 = IR \ {0}.
13.1 Untersuchen Sie das Verhalten von f für x
= IR \ {0}.
13.1 Untersuchen Sie das Verhalten von f für x  ± ∞ sowie für x
± ∞ sowie für x  0!
(Beachten Sie, dass Sie nur einmal die Regel von de L'Hospital brauchen.
Tipp: In diesem Fall formen Sie das Produkt zunächst in einen Quotienten
um.)
0!
(Beachten Sie, dass Sie nur einmal die Regel von de L'Hospital brauchen.
Tipp: In diesem Fall formen Sie das Produkt zunächst in einen Quotienten
um.)  13.2 Bestimmen Sie die Gleichung der schiefen Asymptote des Grafen von f!
13.2 Bestimmen Sie die Gleichung der schiefen Asymptote des Grafen von f!
 13.3 Skizzieren Sie an Hand der gewonnenen Ergebnisse und einer geeigneten
Wertetabelle den Grafen von f!
13.3 Skizzieren Sie an Hand der gewonnenen Ergebnisse und einer geeigneten
Wertetabelle den Grafen von f!  Immer dann, wenn bei einer Funktion f(x) = f1(x)·f2(x) der eine Faktor f1(x)
gegen 0 und der andere Faktor f2(x) gegen –∞ oder gegen +∞ strebt, hilft bei
der Grenzwertbestimmung vielleicht die Regel von de L'Hospital, indem der
Funktionsterm f(x) in einen Quotienten der Form
Immer dann, wenn bei einer Funktion f(x) = f1(x)·f2(x) der eine Faktor f1(x)
gegen 0 und der andere Faktor f2(x) gegen –∞ oder gegen +∞ strebt, hilft bei
der Grenzwertbestimmung vielleicht die Regel von de L'Hospital, indem der
Funktionsterm f(x) in einen Quotienten der Form 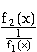 verwandelt wird.
Bearbeiten Sie nun vom Übungsblatt die Aufgabe 5 !
f) Integration
14.1 Bestimmen Sie die folgenden Integrale:
a) ∫exdx ; b) ∫e2xdx ; c) ∫e–x+1dx
verwandelt wird.
Bearbeiten Sie nun vom Übungsblatt die Aufgabe 5 !
f) Integration
14.1 Bestimmen Sie die folgenden Integrale:
a) ∫exdx ; b) ∫e2xdx ; c) ∫e–x+1dx  14.2 Entwickeln Sie eine allgemeine Formel für die Integration des Terms eax+b!
14.2 Entwickeln Sie eine allgemeine Formel für die Integration des Terms eax+b!
 Bearbeiten Sie nun die restlichen Aufgaben 6 bis 15 des Übungsblattes!
Bearbeiten Sie nun die restlichen Aufgaben 6 bis 15 des Übungsblattes!
 ax, x
ax, x  IR.
1. Für welche a
IR.
1. Für welche a  IR ist die allgemeine Exponentialfunktion definiert? Geben Sie
ein Gegenbeispiel an!
IR ist die allgemeine Exponentialfunktion definiert? Geben Sie
ein Gegenbeispiel an!  ax, x
ax, x  IR.
1. Für welche a
IR.
1. Für welche a  IR ist die allgemeine Exponentialfunktion definiert? Geben Sie
ein Gegenbeispiel an!
IR ist die allgemeine Exponentialfunktion definiert? Geben Sie
ein Gegenbeispiel an!  2. Stellen Sie für a = 2 und für a = 3 Wertetabellen der zugehörigen Exponential-
funktionen auf, und zeichnen Sie die Grafen! Beschreiben Sie exakt den Verlauf
beider Grafen, und zwar auch im Verhältnis zueinander!
2. Stellen Sie für a = 2 und für a = 3 Wertetabellen der zugehörigen Exponential-
funktionen auf, und zeichnen Sie die Grafen! Beschreiben Sie exakt den Verlauf
beider Grafen, und zwar auch im Verhältnis zueinander!  b) Die Zahl „e“
Die folgende kleine Bildersequenz zeigt eine interessante Beziehung zwischen den
Grafen ausgewählter Exponentialfunktionen und denen ihrer Ableitungsfunktionen
auf.
Schauen Sie sich nun diese Bildersequenz an!
3. Welche Beziehung zwischen den Grafen der Exponentialfunktionen und denen
ihrer Ableitungsfunktionen fällt in der Bildersequenz auf?
b) Die Zahl „e“
Die folgende kleine Bildersequenz zeigt eine interessante Beziehung zwischen den
Grafen ausgewählter Exponentialfunktionen und denen ihrer Ableitungsfunktionen
auf.
Schauen Sie sich nun diese Bildersequenz an!
3. Welche Beziehung zwischen den Grafen der Exponentialfunktionen und denen
ihrer Ableitungsfunktionen fällt in der Bildersequenz auf?  Sie erkennen, dass es eine Zahl e ≈ 2,75 geben muss, so dass gilt:
Sie erkennen, dass es eine Zahl e ≈ 2,75 geben muss, so dass gilt:
 ex den Differenzenquotienten (d. h. die
Sekantensteigungsformel) auf und klammern Sie e
ex den Differenzenquotienten (d. h. die
Sekantensteigungsformel) auf und klammern Sie e aus!
aus!  0 der Bruch
0 der Bruch 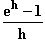 ?
? 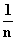 (n = 1; 2; 3; . . .) gegen 0 strebt, kann im Resultat von
Aufgabe 4.3 h durch
(n = 1; 2; 3; . . .) gegen 0 strebt, kann im Resultat von
Aufgabe 4.3 h durch 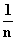 ersetzt werden. Damit ergibt sich für die Zahl e die
berühmte Näherung:
ersetzt werden. Damit ergibt sich für die Zahl e die
berühmte Näherung:
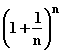
 e (n = 1; 2; 3; . . .)
e (n = 1; 2; 3; . . .) 2x – 3.
5.1 Bestimmen Sie die Gleichung der Funktion g mit der Eigenschaft g(f(x)) = x.
2x – 3.
5.1 Bestimmen Sie die Gleichung der Funktion g mit der Eigenschaft g(f(x)) = x.
 ax, x
ax, x IR
IR 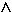 a
a IR+
umkehrbar?
IR+
umkehrbar?  10x, x
10x, x  IR mit ihrer Umkehr-
funktion g.
7.1 Erstellen Sie eine Wertetabelle für die Umkehrfunktion g. Wählen Sie dabei
nur x-Werte, die Zehnerpotenzen darstellen.
7.2 Beschreiben Sie die Wirkung der Funktion g in Worten.
IR mit ihrer Umkehr-
funktion g.
7.1 Erstellen Sie eine Wertetabelle für die Umkehrfunktion g. Wählen Sie dabei
nur x-Werte, die Zehnerpotenzen darstellen.
7.2 Beschreiben Sie die Wirkung der Funktion g in Worten.  IR+, die Umkehrfunktion
g(x) = logax.
Es gilt also:
IR+, die Umkehrfunktion
g(x) = logax.
Es gilt also:
 ex und ihre Derivate zu
untersuchen, da sich alle anderen Exponentialfunktionen auf diese eine zurück-
führen lassen:
ex und ihre Derivate zu
untersuchen, da sich alle anderen Exponentialfunktionen auf diese eine zurück-
führen lassen:
 IR.
Wenn c positiv ist, lässt sich auf beiden Seiten der natürliche Logarithmus
anwenden, und man erhält: g(x) = ln c. Die Lösungen dieser Gleichung sind dann
die Nullstellen der ursprünglichen Exponentialfunktion.
9. Bestimmen Sie die Nullstellen der folgenden Funktionen:
9.1 f: x |
IR.
Wenn c positiv ist, lässt sich auf beiden Seiten der natürliche Logarithmus
anwenden, und man erhält: g(x) = ln c. Die Lösungen dieser Gleichung sind dann
die Nullstellen der ursprünglichen Exponentialfunktion.
9. Bestimmen Sie die Nullstellen der folgenden Funktionen:
9.1 f: x | ex – 1
ex – 1  ex2+1 – e2
ex2+1 – e2  e2x – ex – 2
e2x – ex – 2 
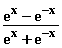
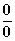 oder
oder 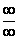 führen.
10.1 Überzeugen Sie sich davon, dass die Funktion f: x |
führen.
10.1 Überzeugen Sie sich davon, dass die Funktion f: x |
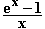 für x
für x  0
einen solchen kniffligen Grenzwert besitzt!
10.2 Ermitteln Sie diesen Grenzwert mit Hilfe des Taschenrechners!
Mit dem Taschenrechner ergibt sich:
0
einen solchen kniffligen Grenzwert besitzt!
10.2 Ermitteln Sie diesen Grenzwert mit Hilfe des Taschenrechners!
Mit dem Taschenrechner ergibt sich: 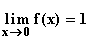 .
Dass wir hier aber nicht auf die empirische Grenzwertermittlung mit dem Taschen-
rechner angewiesen sind, verdanken wir der „Regel von de L'Hospital“.
Sie besagt:
.
Dass wir hier aber nicht auf die empirische Grenzwertermittlung mit dem Taschen-
rechner angewiesen sind, verdanken wir der „Regel von de L'Hospital“.
Sie besagt:

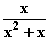 ,
indem Sie den Grenzwert von f an der hebbaren Definitionslücke x = 0
einmal durch Kürzen und zum andern durch Anwendung der Regel von
de L'Hospital bestimmen!
,
indem Sie den Grenzwert von f an der hebbaren Definitionslücke x = 0
einmal durch Kürzen und zum andern durch Anwendung der Regel von
de L'Hospital bestimmen!  0
mit Hilfe der Regel von de L'Hospital!
0
mit Hilfe der Regel von de L'Hospital! 
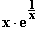 mit ID
mit ID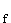 = IR \ {0}.
13.1 Untersuchen Sie das Verhalten von f für x
= IR \ {0}.
13.1 Untersuchen Sie das Verhalten von f für x  ± ∞ sowie für x
± ∞ sowie für x  0!
(Beachten Sie, dass Sie nur einmal die Regel von de L'Hospital brauchen.
Tipp: In diesem Fall formen Sie das Produkt zunächst in einen Quotienten
um.)
0!
(Beachten Sie, dass Sie nur einmal die Regel von de L'Hospital brauchen.
Tipp: In diesem Fall formen Sie das Produkt zunächst in einen Quotienten
um.) 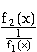 verwandelt wird.
Bearbeiten Sie nun vom Übungsblatt die Aufgabe 5 !
f) Integration
14.1 Bestimmen Sie die folgenden Integrale:
a) ∫exdx ; b) ∫e2xdx ; c) ∫e–x+1dx
verwandelt wird.
Bearbeiten Sie nun vom Übungsblatt die Aufgabe 5 !
f) Integration
14.1 Bestimmen Sie die folgenden Integrale:
a) ∫exdx ; b) ∫e2xdx ; c) ∫e–x+1dx