1. Lösen Sie nach x auf:
a) 10x = 1000 b) 10x = 5 c) ex = 54,6 d) ex = 0,05 e) 2x = 32 f ) 2x = e
 2. Vereinfachen Sie:
a)
2. Vereinfachen Sie:
a) 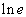 b)
b) 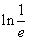 c)
c) 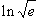 d)
d) 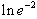 e)
e) 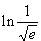 f)
f) 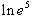 g)
g)  h)
h) 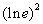 i)
i) 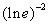 j)
j) 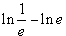
 3. Bestimmen Sie die Lösungen folgender Gleichungen:
a)
3. Bestimmen Sie die Lösungen folgender Gleichungen:
a) 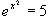 b)
b) 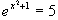 c)
c) 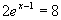 d)
d) 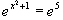 e)
e) 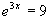 f)
f) 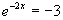 g)
g) 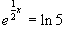 h)
h) 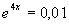 i)
i) 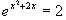 j)
j) 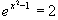 k)
k) 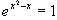
 4. Lösen Sie die Ungleichungen:
a)
4. Lösen Sie die Ungleichungen:
a) 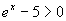 b)
b) 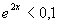 c)
c) 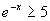 d)
d) 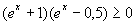 e)
e) 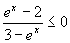 f )
f ) 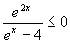
 5. Gegeben sind die folgenden Funktionsgleichungen:
a)
5. Gegeben sind die folgenden Funktionsgleichungen:
a) 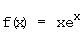 b)
b) 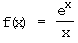 c)
c) 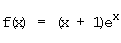 d)
d) 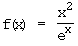 e)
e) 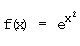 f)
f) 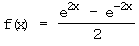 g)
g) 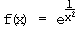 h)
h) 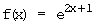 i)
i) 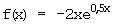 j)
j) 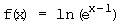 k)
k) 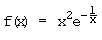 5.1 Bestimmen Sie das Verhalten der Funktionen an ihren Definitionsgrenzen.
5.1 Bestimmen Sie das Verhalten der Funktionen an ihren Definitionsgrenzen.  5.2 Berechnen Sie die Ableitungen.
5.2 Berechnen Sie die Ableitungen.  6. Gegeben ist die Funktion
6. Gegeben ist die Funktion 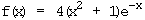 .
6.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x
.
6.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x  ±∞, Nullstellen, Extremwerte
und Wendepunkte.
6.2 Zeichnen Sie den Grafen von f.
6.3 Zeigen Sie, dass
±∞, Nullstellen, Extremwerte
und Wendepunkte.
6.2 Zeichnen Sie den Grafen von f.
6.3 Zeigen Sie, dass 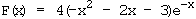 eine Stammfunktion von f ist, und berechnen
Sie den Inhalt der Fläche, die G
eine Stammfunktion von f ist, und berechnen
Sie den Inhalt der Fläche, die G im 1. Quadranten mit der x-Achse einschließt.
im 1. Quadranten mit der x-Achse einschließt.
 7. Gegeben ist die Funktion
7. Gegeben ist die Funktion 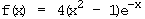 .
7.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x
.
7.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x  ±∞, Nullstellen, Extremwerte
und Wendepunkte.
7.2 Zeichnen Sie den Grafen von f.
7.3 Die Funktion F(x) = (ax2 + bx + c)e–x sei eine Stammfunktion von f. Bestimmen Sie die
Parameter a, b und c, und berechnen Sie dann den Inhalt der Fläche, die G
±∞, Nullstellen, Extremwerte
und Wendepunkte.
7.2 Zeichnen Sie den Grafen von f.
7.3 Die Funktion F(x) = (ax2 + bx + c)e–x sei eine Stammfunktion von f. Bestimmen Sie die
Parameter a, b und c, und berechnen Sie dann den Inhalt der Fläche, die G im 1. Quadranten
mit der x-Achse einschließt.
im 1. Quadranten
mit der x-Achse einschließt.
 8. Gegeben ist die Funktion
8. Gegeben ist die Funktion 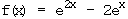 .
8.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x
.
8.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x  ±∞, Nullstellen, Extremwerte
und Wendepunkte.
8.2 Zeichnen Sie den Grafen von f. (1LE = 2cm, Bereich: –3 ≤ x ≤ 1)
8.3 Bestimmen Sie die Menge aller Stammfunktionen von f sowie die Teilmenge derjenigen Stamm-
funktionen, deren Grafen den Grafen von f schneiden.
8.4 Berechnen Sie den Inhalt A(k) der Fläche zwischen G
±∞, Nullstellen, Extremwerte
und Wendepunkte.
8.2 Zeichnen Sie den Grafen von f. (1LE = 2cm, Bereich: –3 ≤ x ≤ 1)
8.3 Bestimmen Sie die Menge aller Stammfunktionen von f sowie die Teilmenge derjenigen Stamm-
funktionen, deren Grafen den Grafen von f schneiden.
8.4 Berechnen Sie den Inhalt A(k) der Fläche zwischen G und der x-Achse, die links von der
Geraden x = k (k < 0) begrenzt wird. Untersuchen Sie das Verhalten von A(k) für k
und der x-Achse, die links von der
Geraden x = k (k < 0) begrenzt wird. Untersuchen Sie das Verhalten von A(k) für k  –∞.
–∞.
 9. Gegeben ist die Funktion
9. Gegeben ist die Funktion 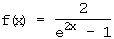 .
9.1 Bestimmen Sie den Definitionsbereich und die Gleichungen aller Asymptoten.
9.2 Untersuchen Sie den Grafen von f auf Horizontalpunkte.
9.3 Zeichnen Sie den Grafen von f. (G
.
9.1 Bestimmen Sie den Definitionsbereich und die Gleichungen aller Asymptoten.
9.2 Untersuchen Sie den Grafen von f auf Horizontalpunkte.
9.3 Zeichnen Sie den Grafen von f. (G hat keine Wendepunkte!)
9.4 Der Graf von f ist symmetrisch. Bestimmen Sie das Symmetrieverhalten so genau wie möglich,
und belegen Sie Ihre Aussage durch eine Rechnung.
9.5 Welcher Grafenpunkt Q ist der Spiegelpunkt zu P(xP | 2) bzgl. der in 9.4 ermittelten Symmetrie?
hat keine Wendepunkte!)
9.4 Der Graf von f ist symmetrisch. Bestimmen Sie das Symmetrieverhalten so genau wie möglich,
und belegen Sie Ihre Aussage durch eine Rechnung.
9.5 Welcher Grafenpunkt Q ist der Spiegelpunkt zu P(xP | 2) bzgl. der in 9.4 ermittelten Symmetrie?
 10. Gegeben ist die Funktion
10. Gegeben ist die Funktion 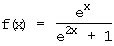 .
10.1 Zeigen Sie, dass G
.
10.1 Zeigen Sie, dass G bzgl. der y-Achse symmetrisch ist.
10.2 Untersuchen Sie das Verhalten der Funktion f an ihren Definitionsgrenzen.
10.3 Ermitteln Sie das Monotonie- und Krümmungsverhalten von f. Geben Sie auch die Art und die
Koordinaten eventueller Horizontal- und Flachpunkte an.
10.4 Zeichnen Sie den Grafen von f. (1LE = 4cm, Bereich: -2 ≤ x ≤ 2)
10.5 Bestimmen Sie die Gleichung einer möglichst einfachen rationalen Funktion g so, dass sich die
Grafen von f und g für –2 ≤ x ≤ 2 nur wenig unterscheiden. Zeichnen Sie den Grafen von g
in ein eigenes Koordinatensystem. (1LE = 4cm, Bereich: -2 ≤ x ≤ 2)
bzgl. der y-Achse symmetrisch ist.
10.2 Untersuchen Sie das Verhalten der Funktion f an ihren Definitionsgrenzen.
10.3 Ermitteln Sie das Monotonie- und Krümmungsverhalten von f. Geben Sie auch die Art und die
Koordinaten eventueller Horizontal- und Flachpunkte an.
10.4 Zeichnen Sie den Grafen von f. (1LE = 4cm, Bereich: -2 ≤ x ≤ 2)
10.5 Bestimmen Sie die Gleichung einer möglichst einfachen rationalen Funktion g so, dass sich die
Grafen von f und g für –2 ≤ x ≤ 2 nur wenig unterscheiden. Zeichnen Sie den Grafen von g
in ein eigenes Koordinatensystem. (1LE = 4cm, Bereich: -2 ≤ x ≤ 2)
 11. Gegeben ist die Funktion
11. Gegeben ist die Funktion 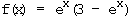 .
11.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x
.
11.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x  ±∞, Nullstellen, Extremwerte
und Wendepunkte.
11.2 Zeichnen Sie den Grafen von f.
11.3 G
±∞, Nullstellen, Extremwerte
und Wendepunkte.
11.2 Zeichnen Sie den Grafen von f.
11.3 G und die Koordinatenachsen schließen im 1. Quadranten eine Fläche ein. Berechnen Sie deren
Inhalt.
11.4 G
und die Koordinatenachsen schließen im 1. Quadranten eine Fläche ein. Berechnen Sie deren
Inhalt.
11.4 G , die y-Achse, die negative x-Achse und die Gerade x = k (k < 0) begrenzen eine Fläche
mit dem Inhalt A(k). Berechnen Sie A(k) und untersuchen Sie dessen Verhalten für k
, die y-Achse, die negative x-Achse und die Gerade x = k (k < 0) begrenzen eine Fläche
mit dem Inhalt A(k). Berechnen Sie A(k) und untersuchen Sie dessen Verhalten für k  –∞.
–∞.
 12. Gegeben ist die Funktion
12. Gegeben ist die Funktion 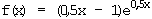 .
12.1 Untersuchen Sie f auf Nullstellen, Grenzverhalten und Asymptoten sowie auf Extremwerte
(Lage und Art).
12.2 Zeichnen Sie Gf im Bereich -4 ≤ x ≤ 4.
12.3 Bestimmen Sie a und b so, dass
.
12.1 Untersuchen Sie f auf Nullstellen, Grenzverhalten und Asymptoten sowie auf Extremwerte
(Lage und Art).
12.2 Zeichnen Sie Gf im Bereich -4 ≤ x ≤ 4.
12.3 Bestimmen Sie a und b so, dass 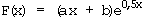 Stammfunktion von f ist.
(Ergebnis: a=1 , b=–4)
12.4 Untersuchen Sie, ob das von Gf , der negativen x-Achse und der y-Achse begrenzte Flächen-
stück einen endlichen Inhalt hat
12.5 Die Punkte O(0 | 0), A(a | f(a)) und B(0 | f(a)) mit 0 < a < 2 bilden ein Dreieck. Bestimmen Sie
den Parameter a so, dass der Flächeninhalt des Dreiecks maximal wird.
Stammfunktion von f ist.
(Ergebnis: a=1 , b=–4)
12.4 Untersuchen Sie, ob das von Gf , der negativen x-Achse und der y-Achse begrenzte Flächen-
stück einen endlichen Inhalt hat
12.5 Die Punkte O(0 | 0), A(a | f(a)) und B(0 | f(a)) mit 0 < a < 2 bilden ein Dreieck. Bestimmen Sie
den Parameter a so, dass der Flächeninhalt des Dreiecks maximal wird.
 13. Gegeben ist die Funktion
13. Gegeben ist die Funktion 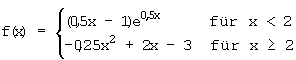 .
13.1 Untersuchen Sie f auf Nullstellen und Extremwerte.
13.2 Untersuchen Sie f an der Stelle x = 2 auf Stetigkeit und auf Differenzierbarkeit.
13.3 Berechnen Sie die Maßzahl der zwischen dem Grafen von f und der positiven x-Achse
eingeschlossenen Fläche. (2 Teilflächen!)
13.4 Begründen Sie, ob es ein c
.
13.1 Untersuchen Sie f auf Nullstellen und Extremwerte.
13.2 Untersuchen Sie f an der Stelle x = 2 auf Stetigkeit und auf Differenzierbarkeit.
13.3 Berechnen Sie die Maßzahl der zwischen dem Grafen von f und der positiven x-Achse
eingeschlossenen Fläche. (2 Teilflächen!)
13.4 Begründen Sie, ob es ein c 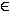 IR gibt, so dass
IR gibt, so dass 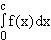 = 0 gilt.
= 0 gilt.
 14. Auf der Erde lebten 1930 etwa 2·109 und 2000 etwa 6·109 Menschen. Das Wachstum
der Erdbevölkerung lässt sich annähernd durch eine Exponentialfunktion der Form n(t) = a · eb t
beschreiben. Dabei bedeuten t die Jahreszahl und n(t) die Anzahl der Menschen im Jahre t.
14.1 Berechnen Sie die rellen Konstanten a und b.
14.2 Wie viele Menschen hätten demnach 1950 gelebt? (Tatsächlicher Wert: 2,509·109)
14.3 Wann wird nach diesem Modell die 10-Milliarden-Grenze überschritten?
14.4 Wann hat nach diesem Modell das biblische Urelternpaar Adam und Eva gelebt?
14.5 In welchem Zeitraum verdoppelt sich demzufolge die Weltbevölkerung?
14.6 Nehmen Sie zu den Grenzen dieses Modells kritisch Stellung.
14. Auf der Erde lebten 1930 etwa 2·109 und 2000 etwa 6·109 Menschen. Das Wachstum
der Erdbevölkerung lässt sich annähernd durch eine Exponentialfunktion der Form n(t) = a · eb t
beschreiben. Dabei bedeuten t die Jahreszahl und n(t) die Anzahl der Menschen im Jahre t.
14.1 Berechnen Sie die rellen Konstanten a und b.
14.2 Wie viele Menschen hätten demnach 1950 gelebt? (Tatsächlicher Wert: 2,509·109)
14.3 Wann wird nach diesem Modell die 10-Milliarden-Grenze überschritten?
14.4 Wann hat nach diesem Modell das biblische Urelternpaar Adam und Eva gelebt?
14.5 In welchem Zeitraum verdoppelt sich demzufolge die Weltbevölkerung?
14.6 Nehmen Sie zu den Grenzen dieses Modells kritisch Stellung.

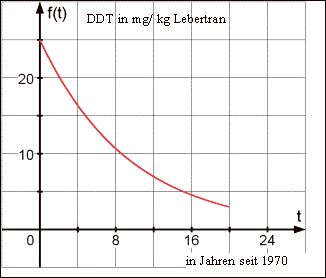
15. (Abschlussprüfung Nachtermin 1999)
In nebenstehendem Diagramm ist eine
Ausgleichskurve für die DDT-Belastung
in Lebertran aus Ostseefischen dargestellt.
Als Ursache für den Rückgang der Be-
lastung wird das Verbot des Einsatzes von
DDT in der Landwirtschaft angesehen.
15.1 Der nebenstehende Graf soll für t ≥ 0
durch eine Exponentialfunktion der Art
f( t ) = a · ek · t mit a, k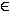 IR beschrieben
werden.
Bestimmen Sie die beiden Koeffizienten
a und k näherungsweise unter Ver-
wendung von geeigneten Daten aus dem
Diagramm. Überprüfen Sie Ihr Ergebnis
an einem weiteren Punktepaar.
(Zur Kontrolle: a = 25, k ≈ –0,107)
15.2 Es gibt eine Zeitspanne T, nach der die DDT-Belastung sich jeweils halbiert hat. Erläutern Sie,
dass hierfür der Ansatz 2f(t0+T) = f(t0) gilt, und berechnen Sie daraus T.
IR beschrieben
werden.
Bestimmen Sie die beiden Koeffizienten
a und k näherungsweise unter Ver-
wendung von geeigneten Daten aus dem
Diagramm. Überprüfen Sie Ihr Ergebnis
an einem weiteren Punktepaar.
(Zur Kontrolle: a = 25, k ≈ –0,107)
15.2 Es gibt eine Zeitspanne T, nach der die DDT-Belastung sich jeweils halbiert hat. Erläutern Sie,
dass hierfür der Ansatz 2f(t0+T) = f(t0) gilt, und berechnen Sie daraus T.
 16. In einer Population von n
16. In einer Population von n =1500 Mitgliedern kann sich eine Epidemie im Verlauf der Zeit t,
gemessen in Tagen, auf folgende drei Arten ausbreiten:
=1500 Mitgliedern kann sich eine Epidemie im Verlauf der Zeit t,
gemessen in Tagen, auf folgende drei Arten ausbreiten:
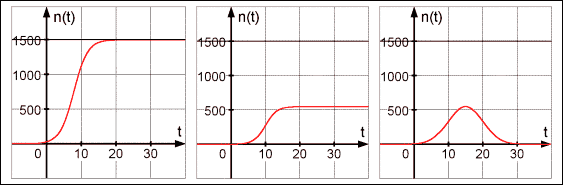 16.1 Erläutern Sie die Unterschiede des Epidemieverlaufs, den die drei Grafen wiedergeben.
Nun sei die Beziehung n(t)=
16.1 Erläutern Sie die Unterschiede des Epidemieverlaufs, den die drei Grafen wiedergeben.
Nun sei die Beziehung n(t)= 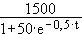 mit t ≥ 0 gegeben. Dabei sei t die Zeit in Tagen.
16.2 Begründen Sie, zu welchem der drei Grafen der Term n(t) nur gehören kann.
16.3 Die Steigung von n an der Stelle t lässt sich als momentane Ausbreitungsgeschwindigkeit der
Epidemie zum Zeitpunkt t interpretieren. Berechnen Sie die Ausbreitungsgeschwindigkeit zum
Zeitpunkt t = 0 sowie den größtmöglichen Wert der Ausbreitungsgeschwindigkeit.
16.4 Berechnen Sie, nach welcher Zeit 60 % der Mitglieder infiziert sind.
mit t ≥ 0 gegeben. Dabei sei t die Zeit in Tagen.
16.2 Begründen Sie, zu welchem der drei Grafen der Term n(t) nur gehören kann.
16.3 Die Steigung von n an der Stelle t lässt sich als momentane Ausbreitungsgeschwindigkeit der
Epidemie zum Zeitpunkt t interpretieren. Berechnen Sie die Ausbreitungsgeschwindigkeit zum
Zeitpunkt t = 0 sowie den größtmöglichen Wert der Ausbreitungsgeschwindigkeit.
16.4 Berechnen Sie, nach welcher Zeit 60 % der Mitglieder infiziert sind.

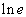 b)
b) 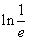 c)
c) 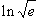 d)
d) 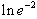 e)
e) 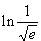 f)
f) 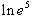 g)
g)  h)
h) 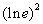 i)
i) 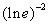 j)
j) 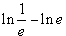
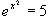 b)
b) 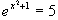 c)
c) 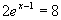 d)
d) 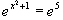 e)
e) 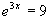 f)
f) 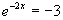 g)
g) 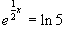 h)
h) 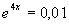 i)
i) 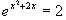 j)
j) 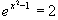 k)
k) 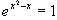
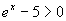 b)
b) 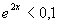 c)
c) 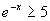 d)
d) 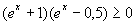 e)
e) 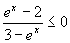 f )
f ) 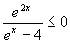
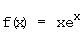 b)
b) 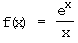 c)
c) 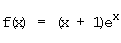 d)
d) 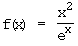 e)
e) 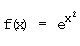 f)
f) 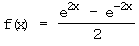 g)
g) 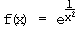 h)
h) 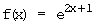 i)
i) 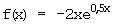 j)
j) 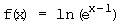 k)
k) 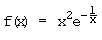 5.1 Bestimmen Sie das Verhalten der Funktionen an ihren Definitionsgrenzen.
5.1 Bestimmen Sie das Verhalten der Funktionen an ihren Definitionsgrenzen. 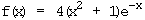 .
6.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x
.
6.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x  ±∞, Nullstellen, Extremwerte
und Wendepunkte.
6.2 Zeichnen Sie den Grafen von f.
6.3 Zeigen Sie, dass
±∞, Nullstellen, Extremwerte
und Wendepunkte.
6.2 Zeichnen Sie den Grafen von f.
6.3 Zeigen Sie, dass 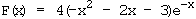 eine Stammfunktion von f ist, und berechnen
Sie den Inhalt der Fläche, die G
eine Stammfunktion von f ist, und berechnen
Sie den Inhalt der Fläche, die G im 1. Quadranten mit der x-Achse einschließt.
im 1. Quadranten mit der x-Achse einschließt.
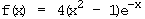 .
7.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x
.
7.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x  ±∞, Nullstellen, Extremwerte
und Wendepunkte.
7.2 Zeichnen Sie den Grafen von f.
7.3 Die Funktion F(x) = (ax2 + bx + c)e–x sei eine Stammfunktion von f. Bestimmen Sie die
Parameter a, b und c, und berechnen Sie dann den Inhalt der Fläche, die G
±∞, Nullstellen, Extremwerte
und Wendepunkte.
7.2 Zeichnen Sie den Grafen von f.
7.3 Die Funktion F(x) = (ax2 + bx + c)e–x sei eine Stammfunktion von f. Bestimmen Sie die
Parameter a, b und c, und berechnen Sie dann den Inhalt der Fläche, die G im 1. Quadranten
mit der x-Achse einschließt.
im 1. Quadranten
mit der x-Achse einschließt.
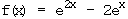 .
8.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x
.
8.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x  ±∞, Nullstellen, Extremwerte
und Wendepunkte.
8.2 Zeichnen Sie den Grafen von f. (1LE = 2cm, Bereich: –3 ≤ x ≤ 1)
8.3 Bestimmen Sie die Menge aller Stammfunktionen von f sowie die Teilmenge derjenigen Stamm-
funktionen, deren Grafen den Grafen von f schneiden.
8.4 Berechnen Sie den Inhalt A(k) der Fläche zwischen G
±∞, Nullstellen, Extremwerte
und Wendepunkte.
8.2 Zeichnen Sie den Grafen von f. (1LE = 2cm, Bereich: –3 ≤ x ≤ 1)
8.3 Bestimmen Sie die Menge aller Stammfunktionen von f sowie die Teilmenge derjenigen Stamm-
funktionen, deren Grafen den Grafen von f schneiden.
8.4 Berechnen Sie den Inhalt A(k) der Fläche zwischen G und der x-Achse, die links von der
Geraden x = k (k < 0) begrenzt wird. Untersuchen Sie das Verhalten von A(k) für k
und der x-Achse, die links von der
Geraden x = k (k < 0) begrenzt wird. Untersuchen Sie das Verhalten von A(k) für k  –∞.
–∞.
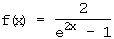 .
9.1 Bestimmen Sie den Definitionsbereich und die Gleichungen aller Asymptoten.
9.2 Untersuchen Sie den Grafen von f auf Horizontalpunkte.
9.3 Zeichnen Sie den Grafen von f. (G
.
9.1 Bestimmen Sie den Definitionsbereich und die Gleichungen aller Asymptoten.
9.2 Untersuchen Sie den Grafen von f auf Horizontalpunkte.
9.3 Zeichnen Sie den Grafen von f. (G hat keine Wendepunkte!)
9.4 Der Graf von f ist symmetrisch. Bestimmen Sie das Symmetrieverhalten so genau wie möglich,
und belegen Sie Ihre Aussage durch eine Rechnung.
9.5 Welcher Grafenpunkt Q ist der Spiegelpunkt zu P(xP | 2) bzgl. der in 9.4 ermittelten Symmetrie?
hat keine Wendepunkte!)
9.4 Der Graf von f ist symmetrisch. Bestimmen Sie das Symmetrieverhalten so genau wie möglich,
und belegen Sie Ihre Aussage durch eine Rechnung.
9.5 Welcher Grafenpunkt Q ist der Spiegelpunkt zu P(xP | 2) bzgl. der in 9.4 ermittelten Symmetrie?
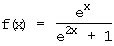 .
10.1 Zeigen Sie, dass G
.
10.1 Zeigen Sie, dass G bzgl. der y-Achse symmetrisch ist.
10.2 Untersuchen Sie das Verhalten der Funktion f an ihren Definitionsgrenzen.
10.3 Ermitteln Sie das Monotonie- und Krümmungsverhalten von f. Geben Sie auch die Art und die
Koordinaten eventueller Horizontal- und Flachpunkte an.
10.4 Zeichnen Sie den Grafen von f. (1LE = 4cm, Bereich: -2 ≤ x ≤ 2)
10.5 Bestimmen Sie die Gleichung einer möglichst einfachen rationalen Funktion g so, dass sich die
Grafen von f und g für –2 ≤ x ≤ 2 nur wenig unterscheiden. Zeichnen Sie den Grafen von g
in ein eigenes Koordinatensystem. (1LE = 4cm, Bereich: -2 ≤ x ≤ 2)
bzgl. der y-Achse symmetrisch ist.
10.2 Untersuchen Sie das Verhalten der Funktion f an ihren Definitionsgrenzen.
10.3 Ermitteln Sie das Monotonie- und Krümmungsverhalten von f. Geben Sie auch die Art und die
Koordinaten eventueller Horizontal- und Flachpunkte an.
10.4 Zeichnen Sie den Grafen von f. (1LE = 4cm, Bereich: -2 ≤ x ≤ 2)
10.5 Bestimmen Sie die Gleichung einer möglichst einfachen rationalen Funktion g so, dass sich die
Grafen von f und g für –2 ≤ x ≤ 2 nur wenig unterscheiden. Zeichnen Sie den Grafen von g
in ein eigenes Koordinatensystem. (1LE = 4cm, Bereich: -2 ≤ x ≤ 2)
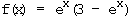 .
11.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x
.
11.1 Diskutieren Sie f in Bezug auf Symmetrie, Verhalten für x  ±∞, Nullstellen, Extremwerte
und Wendepunkte.
11.2 Zeichnen Sie den Grafen von f.
11.3 G
±∞, Nullstellen, Extremwerte
und Wendepunkte.
11.2 Zeichnen Sie den Grafen von f.
11.3 G und die Koordinatenachsen schließen im 1. Quadranten eine Fläche ein. Berechnen Sie deren
Inhalt.
11.4 G
und die Koordinatenachsen schließen im 1. Quadranten eine Fläche ein. Berechnen Sie deren
Inhalt.
11.4 G , die y-Achse, die negative x-Achse und die Gerade x = k (k < 0) begrenzen eine Fläche
mit dem Inhalt A(k). Berechnen Sie A(k) und untersuchen Sie dessen Verhalten für k
, die y-Achse, die negative x-Achse und die Gerade x = k (k < 0) begrenzen eine Fläche
mit dem Inhalt A(k). Berechnen Sie A(k) und untersuchen Sie dessen Verhalten für k  –∞.
–∞.
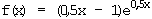 .
12.1 Untersuchen Sie f auf Nullstellen, Grenzverhalten und Asymptoten sowie auf Extremwerte
(Lage und Art).
12.2 Zeichnen Sie Gf im Bereich -4 ≤ x ≤ 4.
12.3 Bestimmen Sie a und b so, dass
.
12.1 Untersuchen Sie f auf Nullstellen, Grenzverhalten und Asymptoten sowie auf Extremwerte
(Lage und Art).
12.2 Zeichnen Sie Gf im Bereich -4 ≤ x ≤ 4.
12.3 Bestimmen Sie a und b so, dass 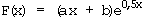 Stammfunktion von f ist.
(Ergebnis: a=1 , b=–4)
12.4 Untersuchen Sie, ob das von Gf , der negativen x-Achse und der y-Achse begrenzte Flächen-
stück einen endlichen Inhalt hat
12.5 Die Punkte O(0 | 0), A(a | f(a)) und B(0 | f(a)) mit 0 < a < 2 bilden ein Dreieck. Bestimmen Sie
den Parameter a so, dass der Flächeninhalt des Dreiecks maximal wird.
Stammfunktion von f ist.
(Ergebnis: a=1 , b=–4)
12.4 Untersuchen Sie, ob das von Gf , der negativen x-Achse und der y-Achse begrenzte Flächen-
stück einen endlichen Inhalt hat
12.5 Die Punkte O(0 | 0), A(a | f(a)) und B(0 | f(a)) mit 0 < a < 2 bilden ein Dreieck. Bestimmen Sie
den Parameter a so, dass der Flächeninhalt des Dreiecks maximal wird.
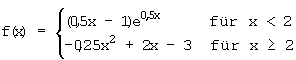 .
13.1 Untersuchen Sie f auf Nullstellen und Extremwerte.
13.2 Untersuchen Sie f an der Stelle x = 2 auf Stetigkeit und auf Differenzierbarkeit.
13.3 Berechnen Sie die Maßzahl der zwischen dem Grafen von f und der positiven x-Achse
eingeschlossenen Fläche. (2 Teilflächen!)
13.4 Begründen Sie, ob es ein c
.
13.1 Untersuchen Sie f auf Nullstellen und Extremwerte.
13.2 Untersuchen Sie f an der Stelle x = 2 auf Stetigkeit und auf Differenzierbarkeit.
13.3 Berechnen Sie die Maßzahl der zwischen dem Grafen von f und der positiven x-Achse
eingeschlossenen Fläche. (2 Teilflächen!)
13.4 Begründen Sie, ob es ein c 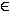 IR gibt, so dass
IR gibt, so dass 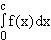 = 0 gilt.
= 0 gilt.

 =1500 Mitgliedern kann sich eine Epidemie im Verlauf der Zeit t,
gemessen in Tagen, auf folgende drei Arten ausbreiten:
=1500 Mitgliedern kann sich eine Epidemie im Verlauf der Zeit t,
gemessen in Tagen, auf folgende drei Arten ausbreiten:
 16.1 Erläutern Sie die Unterschiede des Epidemieverlaufs, den die drei Grafen wiedergeben.
Nun sei die Beziehung n(t)=
16.1 Erläutern Sie die Unterschiede des Epidemieverlaufs, den die drei Grafen wiedergeben.
Nun sei die Beziehung n(t)= 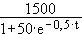 mit t ≥ 0 gegeben. Dabei sei t die Zeit in Tagen.
16.2 Begründen Sie, zu welchem der drei Grafen der Term n(t) nur gehören kann.
16.3 Die Steigung von n an der Stelle t lässt sich als momentane Ausbreitungsgeschwindigkeit der
Epidemie zum Zeitpunkt t interpretieren. Berechnen Sie die Ausbreitungsgeschwindigkeit zum
Zeitpunkt t = 0 sowie den größtmöglichen Wert der Ausbreitungsgeschwindigkeit.
16.4 Berechnen Sie, nach welcher Zeit 60 % der Mitglieder infiziert sind.
mit t ≥ 0 gegeben. Dabei sei t die Zeit in Tagen.
16.2 Begründen Sie, zu welchem der drei Grafen der Term n(t) nur gehören kann.
16.3 Die Steigung von n an der Stelle t lässt sich als momentane Ausbreitungsgeschwindigkeit der
Epidemie zum Zeitpunkt t interpretieren. Berechnen Sie die Ausbreitungsgeschwindigkeit zum
Zeitpunkt t = 0 sowie den größtmöglichen Wert der Ausbreitungsgeschwindigkeit.
16.4 Berechnen Sie, nach welcher Zeit 60 % der Mitglieder infiziert sind.