Wurzeln und Potenzen
Seminararbeit von Sarah Seeger
Dez.2001
Potenzen
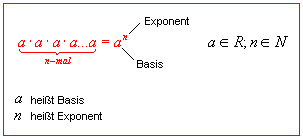
Sie kennen den Potenzbegriff bereits als abkürzende Schreibweise der Multiplikation gleicher Faktoren.
Hier ist n
immer eine Natürliche Zahl.
Diese
Seite gibt eine Einfürung in den Gebrauch von negativen und
gebrochenen Exponenten,
die später als Wurzeln behandelt
werden.
(Alle
Definitionen aus der Formelsammlung „Mathematische Formeln und
Definitionen“, Barth, Mühlbauer, Nikol,
Wörle)
Definitionen
zur
Erweiterung auf alle ganzzahligen Exponenten
Definitionen
zur
Erweiterung auf gebrochene Exponenten
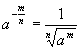
Gebrochene Exponenten können
also auch in Wurzelschreibweise dargestellt werden.
Näheres erfahren sie bei Wurzeln
weiter unten.
Rechengesetze
Faustregel:
Treten mehrere Rechenregeln gemeinsam auf so
gilt:
Klammer
vor Potenz,
Potenz
vor Punkt,
Punkt
vor Strich!
Multiplizieren von
Potenzen mit gleicher Basis
Multiplizieren von
Potenzen mit gleichem Exponenten
Division von
Potenzen mit gleicher Basis
Division von
Potenzen mit gleichem Exponenten
Sie
kennen bereits
als
genau diejenige Zahl, die mit sich selbst multipliziert x
ergibt.
|
|
|
Das
Radizieren (=Wurzelziehen)
ist die Umkehrung zum Potenzieren,
beide Rechenoperationen heben
sich also gegenseitig auf
Definition
zur
Erweiterung der Quadratwurzel auf allgemeine Wurzeln
; 
Nomenklatur: 
heißt
n-te Wurzel aus a
Rechengesetze
Multiplikation
gleicher Wurzeln
"Erweitern"
und "Kürzen" von Wurzeln
Teilweises
Radizieren bzw. „ unter die Wurzel ziehen“
Achtung:
Häufige Fehler!
|
|
|
|
|
|
|
|
|
Festigen
Sie Ihre Erkenntnisse auf dem Übungsblatt zu Wurzeln und Potenzen!
Weitere
Links zum Thema Mathematik
