11. Klasse 3. Schulaufgabe 28.06.2007
     

 
1.  
1.1 In der Formelsammlung (S.27) steht die Höhenformel des gleichschenkligen Dreiecks. Man setzt für a die 10 cm ein. Somit erhält man die Höhe des Dreiecks.

1.2

Um die Höhe der Pyramide zu erhalten, wird der Satz des Pythagoras in dem gestrichelt eingezeichneten Dreieck angewendet. Die Kathete in der Grundfläche hat die Länge 0,5a , also 5 cm.
1.3

Nun können die berechneten Werte in die Volumenformel der Pyramide V = eingesetzt werden.

Die Oberfläche wird so berechnet, dass man die Flächen der vier gleichgroßen Dreiecke und das Quadrat ( das die Grundfläche darstellt) addiert.

     
     
2  
 

Dies ist die faktorisierte Form, die Nullstellen sind aus den Klammern abzulesen.

Den x-Wert des Scheitels erhält man, indem man den Mittelwert zwischen den Nullstellen berechnet . Diesen setzt man in die faktorisierte Form der Gleichung ein und erhält den y-Wert des Scheitelpunktes.

 
     

3.

  
3.1

Das Ziel hier ist, drei Gleichungen aufzustellen, um die gesuchte Funktionsgleichung zu finden. Diese erhält man durch einsetzen der 3 gegebenen Punkte in die allgemeine Gleichung einer Parabel .

Das gesuchte c wird erkennbar, wenn man den Punkt (0/1) einsetzt. Es bleiben 2 Gleichungen übrig. Nun kann man b in Abhängigkeit von a ausrechnen. Diese setzt man in die zweite Gleichung ein und man erhält a. Nun kann b berechnet werden. Sind alle Parameter ausgerechnet, kann die gesuchte Funktionsgleichung aufgestellt werden.

 

3.2

Den Scheitel erhält man, wenn man die allgemeine Scheitelform xs = benutzt. Hier setzt man a und b aus 3.1) ein. So erhält man den x-Wert des Scheitels. Diesen setzt man in die Funktion ein und erhält den y-Wert. Die Nullstellen lassen sich mit der Mitternachtsformel errechnen.


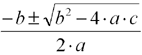3.3 Hier setzt man die Parabel p mit der Geraden g gleich. Dann kann man mit Hilfe der Mitternachtsformel x1,2 = die Lösung bestimmen.
3.4  
a weil sie eine Parabel gleicher Form, nur um 1 LE in Richtung der y-Achse verschoben ist  
b die Parabel besitzt den selben Wert a = - 0,5 und deshalb gibt es nur einen Schnittpunkt  
c die Parabel ist durch Spiegelung an der x-Achse aus der gegebenen entstanden  
     
     
     
4. Gegeben ist die Parabelschar
 
4.1 Sie gehen alle bei -3 durch die y-Achse; das a variiert und somit können verschiedene Parabeln entstehen.

4.2 Es wäre keine Parabel.
4.3 Für a < 0 sind die Parabeln nach unten offen und da der Scheitel auch unterhalb der x-Achse liegt, kann es keine Nullstellen geben.
4.4 Es muss die Parabel mit der Geraden gleichgesetzt werden . Für die entstehende quadratische Gleichung kann die Diskriminante berechnet werden. Es muss genau eine Lösung ergeben, d.h. die Diskriminante muss Null sein (a=0,5). Dann kann a eingesetzt und der Berührpunkt errechnet werden.
     
     
5. Die Kugel schafft es über die erste Spitze, aber nicht über die zweite Spitze und bleibt somit dazwischen liegen. Der Beweis dafür ist, dass der Scheitelpunkt der Wurfbahn bei (3/6), also in gleicher Höhe aber vor der zweiten Spitze liegt. Somit schafft die Kugel die zweite Spitze nicht, sie fällt in die Mulde zwischen den Gipfeln.