Nachbearbeitung und Ergänzung: OStR Starfinger
| a) | 2x – 2y – 6 = 0 | b) | 5x – 3y = –4 | c) | 9x + 208y – 15 = 0 | ||||||||
| x + 2y = 0 | 12x + 3y = –3 | –9x + 72y – 55 = 0 | |||||||||||
 |
|||||||||||||
| d) | 5x – 3y = 10 | e) | x –4·(1 – y) = 3 + 3y | f) | 1,21x = 45,2y + 13,1 | ||||||||
| x – 20 = –1,5y | 3·(x + 1) – y = 6 + 2x | 1,21x = 20,4y + 11,7 | |||||||||||
| a) | 2x + 2y – 2z = 14 | b) | 3x – 5y + 10z = 17 | c) | 3x – y + 4z = 24 | ||||||||
| 2x – y + z = 8 | x + y + z = 43 | x – y + z = 8 | |||||||||||
| 3x + 2y – z = 20 | –x + y – z = –3 | 6x – 4y + 5z = 40 | |||||||||||
| |
|||||||||||||
| d) | 2x + y – z = 7 | e) | 2x + y – z = 0 | f) | 4x – 3y + 2z = 208 | ||||||||
| x – 3y – 2z = –3 | 3x – 2y + z = 11 | 8x – 6y + 5z = 481 | |||||||||||
| 5x + 3y + z = 2 | x – y + 2z = 9 | 2x + 5y – 8z = 390 | |||||||||||
| a) | 2x + 2y = –16 | b) | 7y – 3x = 6 | c) | x = 3y – 4 | ||||||||
| 2x – 2y = 4 | 3x + 2y = 3 | 3x – 5y = –4 | |||||||||||
| |
|||||||||||||
| d) | 0,5x + 2y – 5 = 0 | e) | y = 1,5x + 2 | f) | y = 3,57x – 1,11 | ||||||||
| 0,25x – 1,5y – 2 = 0 | y + 1,25x + 3 = 0 | y = 1,35x + 3,55 | |||||||||||
| a) | 2x + 2y – 2z = 14 | b) | 2x + y – z = 7 | c) | 3x – y + 4z = 24 | |
||||||||
| 2x – y + z = 8 | x – 3y – 2z = –3 | x – y + z = 8 | ||||||||||||
| 3x + 2y – z = 20 | 5x + 3y + z = 2 | 6x – 4y + 5z = 40 |
Lösen Sie das folgende Gleichungssystem mit 3 Variablen nach dem Gleichsetzungs- verfahren:
|
c = a + b – 7
|
|
|||
| c = 8 – b – a | ||||
| c = 3a + 2b – 20 |
In einem Behälter befinden sich 3 verschiedene Kugelsorten: leichte blaue, schwerere grüne und noch schwerere rote Kugeln, deren Massen bestimmt werden sollen. Zur Verfügung stehen eine Balkenwaage sowie ein Gewicht von 1 kg. Es wird festgestellt:
- Gleichfarbige Kugeln sind gleich schwer.
- 5 grüne und 2 blaue Kugeln wiegen genau so viel wie 3 rote Kugeln.
- 3 grüne Kugeln wiegen genau so viel wie 1 rote und 2 blaue Kugeln.
- 1 grüne und 2 blaue Kugeln wiegen 1 kg.
Ein Eisenwarenproduzent möchte Verkaufspackungen zusammenstellen, die außer Nägeln eine bestimmten Sorte Maschinenschrauben und eine gleiche Anzahl dazu passender Muttern enthalten sollen. Dabei sollen sich in jeder Packung mit einer Gesamtmasse von 1,5 kg insgesamt 100 Einzelteile befinden.
Ermitteln Sie unter der Voraussetzung, dass die Masse eines Nagels 25 g, einer Schraube 20 g und einer Mutter 5 g beträgt, die Anzahl der Nägel, Schrauben und Muttern je Packung!
Wie viele Nägel, Schrauben und Muttern befinden sich in einer Packung, wenn die Masse eines Nagels 15 g, einer Schraube 20 g und einer Mutter 10 g beträgt? Erläutern Sie das überraschende Ergebnis!
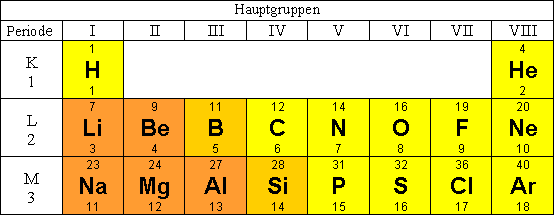
Drei chemische Elemente, die zunächst mit den Symbolen X, Y und Z bezeichnet werden sollen, bilden drei verschiedene Verbindungen mit den Bruttoformeln X3YZ, XYZ3 und X4Y2Z3. Die Molekülmassen dieser Verbindungen betragen in der selben Reihenfolge
Bestimmen Sie die Atommassen der Elemente X, Y und Z und entnehmen Sie dem abgebildeten Auszug aus dem Periodensystem, um welche Elemente es sich dabei handelt. (Hinweis: Die Atommasse steht über dem jeweiligen Elementsymbol.)
9.
Ein Schwimmwettkampf wird auf einem Fluss ausgetragen und dazu eine 100m lange Strecke am Flussufer markiert. Ein Schwimmer legt die Strecke zunächst flussabwärts in 66 s zurück, beim Rückweg flussaufwärts braucht aber 100 s, obwohl er gleich schnell schwimmt wie vorher.
Berechnen Sie die Fließgeschwindigkeit des Flusses und die Eigengeschwindigkeit des Schwimmers.
Lösung: Fluss: 0,25 m / s , Schwimmer: 1,25 m / s