1. Gegeben ist die reelle Funktion g: xg(x),

   mit g(x) =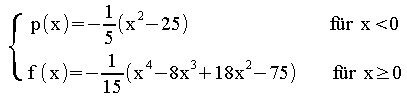

   Überprüfen Sie rechnerisch, ob die Funktion g an der Stelle x₀= 0 stetig und differenzierbar ist.

   

   ---

2. Gegeben ist die reelle Funktion g: xg(x),

   mit g(x) =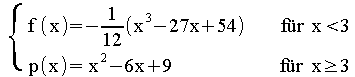

   Überprüfen Sie rechnerisch, ob die Funktion g an der Stelle x₀= 3 stetig und differenzierbar ist.

   

   ---

3. Gegeben ist die reelle Funktion f: xf(x),

   mit f(x) =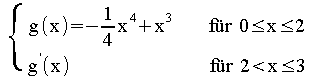

   Überprüfen Sie rechnerisch, ob die in ihrer Definitionsmenge stetige Funktion f an der Stelle x₀= 2 differenzierbar ist.

   

   ---

4. Gegeben ist die reelle Funktion k: xk(x),

   mit k(x) =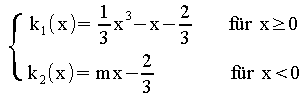

   Berechnen Sie m so, dass die für alle m stetige Funktion k an der

   Stelle x₀= 0 differenzierbar ist.

   

   ---

5. Gegeben ist die reelle Funktion g: xg(x),

   mit g(x) =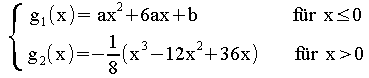

   Berechnen Sie a und b so, dass Funktion g an der Stelle x₀= 0 stetig und differenzierbar ist.

   

   ---

6. Gegeben ist die reelle Funktion k: xk(x),

   mit k(x) =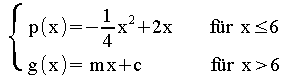

   Berechnen Sie den Term g(x) so, dass die Funktion k an der Stelle x₀= 6 stetig und differenzierbar ist.

   

   ---

7. Gegeben ist die reelle Funktion g: xg(x),

   mit g(x) =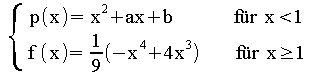

   Berechnen Sie den Term p(x) so, dass die Funktion g an der Stelle x₀= 1 stetig und differenzierbar ist.

   

   ---

8. Einem Betrieb entstehen bei der Herstellung einer Ware Gesamtkosten, die von

   der Menge des hergestellten Produkts (kurz: Produktmenge x) abhängen.

   Für die Produktion ergibt sich folgende Kostenfunktion f: xf(x),

   für die gilt:

   f(x) =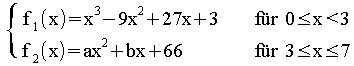

   Berechnen Sie a und b so, dass die Funktion f an der Stelle x₀= 3 stetig und differenzierbar ist.

   Erläutern Sie, was die Stetigkeit der Funktion f an der Stelle x₀= 3 im Sinne der vorliegenden Thematik bedeutet.

   

         Anfang