Begründen Sie, dass nachfolgende Funktionen im jeweils angegebenen Intervall I genau eine Nullstelle besitzen, und bestimmen Sie nach dem NNV jeweils diese Nullstelle auf 2 Nachkommastellen genau!
| a) f(x) = x3 – 2x2 – 5x – 3; I = [3;4] |  | b) f(x) = x3 – x2 – 8x – 7; I = [3;4] |
| c) f(x) = x5 – 3x3 + 5; I = [–2;–1,5] | d) f(x) = x5 + x3 – 4; I = [1;2] |
Mit Hilfe des NNV möchte man eine Nullstelle der Funktion fa(x) = ax3 – x2 + 2x – a, a > 0, im Intervall I = [0;1] bestimmen. Mit dem Startwert z1 =1 erhält man das Folgeglied z2 = 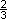 . Bestimmen Sie den Parameter a!
. Bestimmen Sie den Parameter a! 
Bestimmen Sie nach dem NNV die folgenden Wurzeln auf 2 Nachkommastellen genau!
Mit dem Startwert z1 =1 erhält jemand beim NNV die beiden Folgeglieder z2 =4 und z3 = 3. Skizzieren Sie einen dazu passenden Kurvenausschnitt der zugrundeliegenden Funktion, und tragen Sie die zugehörigen Tangenten ein! 
Gegeben ist eine Funktion f mit den Nullstellen x1 = –2 und x2 = 3. Die Zahlenfolge eines durchgeführten NNV beginnt mit z1 = 4; z2 = –3; z3 = –2,5; ... Skizzieren Sie ein dazu passendes Stück des Graphen von f mitsamt den zugehörigen Tangenten! 
Jemand behauptet, das NNV führe stets zu einer Nullstelle der vorgegebenen Funktion, falls diese überhaupt Nullstellen besitzt. Widerlegen Sie die Behauptung zeichnerisch an einem geeigneten Kurvenbeispiel! 
Bei der Berechnung eines NNV–Folgegliedes zn zeigt der Taschenrechner trotz korrekter Eingabe "–E–". Was könnte passiert sein? 
Bei zwei Funktionen f1 und f2 wird zur Nullstellenbestimmung das NNV durchgeführt. Dabei beginnen die Zahlenfolgen wie folgt: F1: 4, 2, 2,5 . . .; F2: 4, 3, 2,5 . . .
Was lässt sich jeweils über den Verlauf der Graphen aussagen? 
Bei der Funktion f(x) = 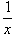 führt das NNV mit jedem von Null verschiedenen Startwert zu einer Zahlenfolge, die entweder nach +∞ oder nach –∞ läuft.
führt das NNV mit jedem von Null verschiedenen Startwert zu einer Zahlenfolge, die entweder nach +∞ oder nach –∞ läuft.
|
| 9.1 | Überzeugen Sie sich anhand einer Skizze von der Richtigkeit der Aussage!  |
| 9.2 | Untersuchen und begründen Sie, ob es auch Polynomfunktionen mit dieser Eigenschaft gibt!  |
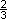 . Bestimmen Sie den Parameter a!
. Bestimmen Sie den Parameter a! 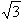
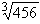
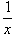 führt das NNV mit jedem von Null verschiedenen Startwert zu einer Zahlenfolge, die entweder nach +∞ oder nach –∞ läuft.
führt das NNV mit jedem von Null verschiedenen Startwert zu einer Zahlenfolge, die entweder nach +∞ oder nach –∞ läuft.