Arbeitsblatt Natürlicher Logarithmus
OStR Starfinger
a) Wiederholung
1.1 Erklären Sie, um welche Funktion es sich bei dem „natürlichen Logarithmus“
handelt!  1.2 In welcher geometrischen Beziehung stehen die Grafen der e-Funktion und
des natürlichen Logarithmus miteinander?
1.2 In welcher geometrischen Beziehung stehen die Grafen der e-Funktion und
des natürlichen Logarithmus miteinander?  1.3 Zeichnen Sie den Grafen der Funktion f(x) = ln x !
1.3 Zeichnen Sie den Grafen der Funktion f(x) = ln x !  1.4 Leiten Sie aus dem Grafen von 1.3 möglichst viele Eigenschaften der Funktion
f(x) = ln x ab!
1.4 Leiten Sie aus dem Grafen von 1.3 möglichst viele Eigenschaften der Funktion
f(x) = ln x ab!  b) Nullstellenbestimmung
Bei der Nullstellenbestimmung einer Funktion mit dem natürlichen Logarithmus
ergibt sich nach eventueller Umformung oft eine logarithmische Gleichung
der Form
ln(g(x)) = c mit c
b) Nullstellenbestimmung
Bei der Nullstellenbestimmung einer Funktion mit dem natürlichen Logarithmus
ergibt sich nach eventueller Umformung oft eine logarithmische Gleichung
der Form
ln(g(x)) = c mit c  IR.
Auf die beiden Seiten dieser Gleichung lässt sich die e-Funktion als Umkehr-
funktion des natürlichen Logarithmus anwenden, und man erhält:
g(x) = ec.
Die Lösungen dieser Gleichung sind dann die Nullstellen der ursprünglichen
Logarithmusfunktion.
2. Bestimmen Sie die Definitionsmengen und die Nullstellen der folgenden
Funktionen:
2.1 f: x |
IR.
Auf die beiden Seiten dieser Gleichung lässt sich die e-Funktion als Umkehr-
funktion des natürlichen Logarithmus anwenden, und man erhält:
g(x) = ec.
Die Lösungen dieser Gleichung sind dann die Nullstellen der ursprünglichen
Logarithmusfunktion.
2. Bestimmen Sie die Definitionsmengen und die Nullstellen der folgenden
Funktionen:
2.1 f: x | ln x – 1
ln x – 1  2.2 f: x |
2.2 f: x | ln(x2–1) – ln 3
ln(x2–1) – ln 3  2.3 f: x |
2.3 f: x | (ln x)2 + ln x – 2
(ln x)2 + ln x – 2  2.4 f: x |
2.4 f: x | (x2 – 1)·ln(x2 + 1,5x)
(x2 – 1)·ln(x2 + 1,5x)  Bearbeiten Sie nun vom Übungsblatt die Aufgabe 1 !
c) Ableitung des natürlichen Logarithmus
Die Funktion f(x) = x lässt sich zumindest für x > 0 etwas kompliziert als
f(x) = eln x darstellen.
3. Leiten Sie beide Darstellungsweisen der Funktion f ab, und vereinfachen Sie
das Ergebnis!
Welche Schlussfolgerung ergibt sich für die Ableitung (ln x)' von ln x?
Bearbeiten Sie nun vom Übungsblatt die Aufgabe 1 !
c) Ableitung des natürlichen Logarithmus
Die Funktion f(x) = x lässt sich zumindest für x > 0 etwas kompliziert als
f(x) = eln x darstellen.
3. Leiten Sie beide Darstellungsweisen der Funktion f ab, und vereinfachen Sie
das Ergebnis!
Welche Schlussfolgerung ergibt sich für die Ableitung (ln x)' von ln x?  4. Bestimmen Sie die Ableitungen der Funktionen von Aufgabe 2!
4. Bestimmen Sie die Ableitungen der Funktionen von Aufgabe 2!  Bearbeiten Sie nun vom Übungsblatt die Aufgabe 2 !
d) Rechenregeln für den Logarithmus
Der Begriff „Logarithmus“ ist ein Synonym für „Exponent“. Beispielsweise ist
der Zehnerlogarithmus von 1000 gleich dem Exponenten, mit dem 10 potenziert
werden muss, um 1000 zu erhalten. Demnach müssen die bekannten Potenz-
regeln zum Multiplizieren oder Dividieren von Potenzen mit gleicher Basis sowie
zum Potenzieren von Potenzen in analoger Weise als Rechenregeln für den
Logarithmus formulierbar sein.
5. Stellen Sie in einer Tabelle die erwähnten Potenzregeln und die dazu analogen
Logarithmusregeln zusammen!
Bearbeiten Sie nun vom Übungsblatt die Aufgabe 2 !
d) Rechenregeln für den Logarithmus
Der Begriff „Logarithmus“ ist ein Synonym für „Exponent“. Beispielsweise ist
der Zehnerlogarithmus von 1000 gleich dem Exponenten, mit dem 10 potenziert
werden muss, um 1000 zu erhalten. Demnach müssen die bekannten Potenz-
regeln zum Multiplizieren oder Dividieren von Potenzen mit gleicher Basis sowie
zum Potenzieren von Potenzen in analoger Weise als Rechenregeln für den
Logarithmus formulierbar sein.
5. Stellen Sie in einer Tabelle die erwähnten Potenzregeln und die dazu analogen
Logarithmusregeln zusammen!  Der Logarithmus verwandelt also Produkte in Summen, Quotienten in Differenzen
und Potenzen in Produkte, d. h. er führt eine höhere Rechenart auf die nächst
einfachere Rechenart zurück.
6.1 Welche geometrische Beziehung besteht zwischen den Grafen der Funktionen
f(x) = ln x und g(x) = ln 2x ?
Der Logarithmus verwandelt also Produkte in Summen, Quotienten in Differenzen
und Potenzen in Produkte, d. h. er führt eine höhere Rechenart auf die nächst
einfachere Rechenart zurück.
6.1 Welche geometrische Beziehung besteht zwischen den Grafen der Funktionen
f(x) = ln x und g(x) = ln 2x ?  6.2 Welche geometrische Beziehung besteht zwischen den Grafen der Funktionen
f(x) = ln x² und g(x) = 2 ln x ?
6.2 Welche geometrische Beziehung besteht zwischen den Grafen der Funktionen
f(x) = ln x² und g(x) = 2 ln x ?  6.3 Welche geometrische Beziehung besteht zwischen den Grafen der Funktionen
f(x) = ln x² und g(x) = 2 ln |x| ?
6.3 Welche geometrische Beziehung besteht zwischen den Grafen der Funktionen
f(x) = ln x² und g(x) = 2 ln |x| ?  7. Jemand behauptet, auf Grund der Rechenregeln zum Logarithmus gelte
ln
7. Jemand behauptet, auf Grund der Rechenregeln zum Logarithmus gelte
ln 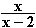 = ln x – ln (x – 2). Widerlegen und korrigieren Sie diese Behauptung!
= ln x – ln (x – 2). Widerlegen und korrigieren Sie diese Behauptung!
 Aus den Aufgaben 6.2 und 7. wird deutlich, dass bei der Anwendung der
Logarithmus-Rechenregeln auf logarithmische Funktionsterme Vorsicht geboten
ist, da sich bei Unachtsamkeit leicht die Definitionsmenge verändern kann.
Bearbeiten Sie nun vom Übungsblatt die Aufgaben 3 und 4 !
e) Knifflige Grenzwerte
Wie bei der e-Funktion können auch beim natürlichen Logarithmus Grenzwerte
auftreten, die die Form
Aus den Aufgaben 6.2 und 7. wird deutlich, dass bei der Anwendung der
Logarithmus-Rechenregeln auf logarithmische Funktionsterme Vorsicht geboten
ist, da sich bei Unachtsamkeit leicht die Definitionsmenge verändern kann.
Bearbeiten Sie nun vom Übungsblatt die Aufgaben 3 und 4 !
e) Knifflige Grenzwerte
Wie bei der e-Funktion können auch beim natürlichen Logarithmus Grenzwerte
auftreten, die die Form 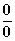 oder
oder 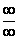 haben. Auch hier hilft oft die Regel von
de L'Hospital!
8. Untersuchen Sie das Verhalten der folgenden Funktionen an ihren
Definitionsrändern:
8.1 f: x |
haben. Auch hier hilft oft die Regel von
de L'Hospital!
8. Untersuchen Sie das Verhalten der folgenden Funktionen an ihren
Definitionsrändern:
8.1 f: x |
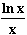
 8.2 f: x |
8.2 f: x |
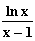
 8.3 f: x |
8.3 f: x | x · ln x
x · ln x  Bearbeiten Sie nun vom Übungsblatt die Aufgabe 5 !
f) Der natürliche Logarithmus als Stammfunktion
9.1 Bestimmen Sie die folgenden Integrale:
a) ∫
Bearbeiten Sie nun vom Übungsblatt die Aufgabe 5 !
f) Der natürliche Logarithmus als Stammfunktion
9.1 Bestimmen Sie die folgenden Integrale:
a) ∫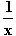 dx für x > 0; b) ∫
dx für x > 0; b) ∫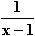 dx für x > 1; c) ∫
dx für x > 1; c) ∫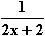 dx für x > –1;
d) ∫
dx für x > –1;
d) ∫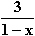 dx für x < 1; e) ∫
dx für x < 1; e) ∫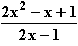 dx für x > 0,5
dx für x > 0,5  9.2 Stellen Sie eine allgemeine Formel zur Berechnung des Integrals
9.2 Stellen Sie eine allgemeine Formel zur Berechnung des Integrals
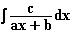 für a, c
für a, c  IR\{0}, b
IR\{0}, b  IR und ax + b > 0 auf!
IR und ax + b > 0 auf!  10.1 Leiten Sie ab:
a) ln x für x > 0; b) ln (–x) für x < 0;
c) ln (x–1) für x > 1; d) ln (1–x) für x < 1;
e) ln (2x+4) für x > –2; f) ln (–2x–4) für x < –2
10.1 Leiten Sie ab:
a) ln x für x > 0; b) ln (–x) für x < 0;
c) ln (x–1) für x > 1; d) ln (1–x) für x < 1;
e) ln (2x+4) für x > –2; f) ln (–2x–4) für x < –2  10.2 Geben Sie nun jeweils eine Stammfunktion F der folgenden Funktionen an:
a) f(x) =
10.2 Geben Sie nun jeweils eine Stammfunktion F der folgenden Funktionen an:
a) f(x) = 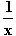 , x
, x  IR\{0}; b) f(x) =
IR\{0}; b) f(x) = 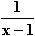 , x
, x  IR\{1}
c) f(x) =
IR\{1}
c) f(x) = 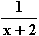 , x
, x  IR\{–2}; d) f(x) =
IR\{–2}; d) f(x) = 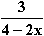 , x
, x  IR\{2}
IR\{2}  Bearbeiten Sie nun die restlichen Aufgaben 6 bis 15 des Übungsblattes!
Bearbeiten Sie nun die restlichen Aufgaben 6 bis 15 des Übungsblattes!
 IR.
Auf die beiden Seiten dieser Gleichung lässt sich die e-Funktion als Umkehr-
funktion des natürlichen Logarithmus anwenden, und man erhält:
g(x) = ec.
Die Lösungen dieser Gleichung sind dann die Nullstellen der ursprünglichen
Logarithmusfunktion.
2. Bestimmen Sie die Definitionsmengen und die Nullstellen der folgenden
Funktionen:
2.1 f: x |
IR.
Auf die beiden Seiten dieser Gleichung lässt sich die e-Funktion als Umkehr-
funktion des natürlichen Logarithmus anwenden, und man erhält:
g(x) = ec.
Die Lösungen dieser Gleichung sind dann die Nullstellen der ursprünglichen
Logarithmusfunktion.
2. Bestimmen Sie die Definitionsmengen und die Nullstellen der folgenden
Funktionen:
2.1 f: x | ln x – 1
ln x – 1  ln(x2–1) – ln 3
ln(x2–1) – ln 3  (ln x)2 + ln x – 2
(ln x)2 + ln x – 2  (x2 – 1)·ln(x2 + 1,5x)
(x2 – 1)·ln(x2 + 1,5x) 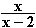 = ln x – ln (x – 2). Widerlegen und korrigieren Sie diese Behauptung!
= ln x – ln (x – 2). Widerlegen und korrigieren Sie diese Behauptung!
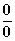 oder
oder 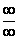 haben. Auch hier hilft oft die Regel von
de L'Hospital!
8. Untersuchen Sie das Verhalten der folgenden Funktionen an ihren
Definitionsrändern:
8.1 f: x |
haben. Auch hier hilft oft die Regel von
de L'Hospital!
8. Untersuchen Sie das Verhalten der folgenden Funktionen an ihren
Definitionsrändern:
8.1 f: x |
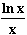

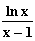
 x · ln x
x · ln x 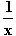 dx für x > 0; b) ∫
dx für x > 0; b) ∫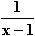 dx für x > 1; c) ∫
dx für x > 1; c) ∫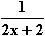 dx für x > –1;
d) ∫
dx für x > –1;
d) ∫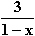 dx für x < 1; e) ∫
dx für x < 1; e) ∫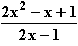 dx für x > 0,5
dx für x > 0,5 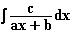 für a, c
für a, c  IR\{0}, b
IR\{0}, b  IR und ax + b > 0 auf!
IR und ax + b > 0 auf! 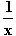 , x
, x  IR\{0}; b) f(x) =
IR\{0}; b) f(x) = 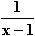 , x
, x  IR\{1}
c) f(x) =
IR\{1}
c) f(x) = 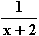 , x
, x  IR\{–2}; d) f(x) =
IR\{–2}; d) f(x) = 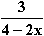 , x
, x  IR\{2}
IR\{2}