9. Gegeben ist die Funktion f: x 
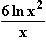 .
9.1 Diskutieren Sie f in Bezug auf den max. Definitionsbereich, Symmetrie, Verhalten an
den Rändern des Definitionsbereichs, Asymptoten, Nullstellen sowie Extrem- und
Wendepunkte.
9.2 Zeichnen Sie den Grafen von f.
9.3 Aus der Funktion f soll eine abschnittsweise definierte Funktion g gewonnen werden,
die die Polstelle von f „überbrückt“. Dazu soll diejenige Gerade aus der Schar y = mx,
die die Äste des Grafen von f berührt, zwischen den Berührpunkten den Grafen von f
ersetzen. Ermitteln Sie diese Gerade, und geben Sie die Funktionsgleichung der
Funktion g an!
.
9.1 Diskutieren Sie f in Bezug auf den max. Definitionsbereich, Symmetrie, Verhalten an
den Rändern des Definitionsbereichs, Asymptoten, Nullstellen sowie Extrem- und
Wendepunkte.
9.2 Zeichnen Sie den Grafen von f.
9.3 Aus der Funktion f soll eine abschnittsweise definierte Funktion g gewonnen werden,
die die Polstelle von f „überbrückt“. Dazu soll diejenige Gerade aus der Schar y = mx,
die die Äste des Grafen von f berührt, zwischen den Berührpunkten den Grafen von f
ersetzen. Ermitteln Sie diese Gerade, und geben Sie die Funktionsgleichung der
Funktion g an!
 10. Gegeben ist die Funktion f: x
10. Gegeben ist die Funktion f: x 
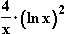 .
10.1 Geben Sie den maximalen Definitionsbereich von f an!
10.2 Untersuchen Sie das Verhalten der Funktion f an ihren Definitionsgrenzen, und geben
Sie die Gleichungen der Asymptoten ihres Grafen an.
10.3 Ermitteln Sie das Monotonie- und Krümmungsverhalten von f. Geben Sie auch die Art
und die Koordinaten eventueller Horizontal- und Flachpunkte an.
10.4 Zeichnen Sie den Grafen von f für x ≤ 10.
10.5 In einer Integral-Formelsammlung steht:
.
10.1 Geben Sie den maximalen Definitionsbereich von f an!
10.2 Untersuchen Sie das Verhalten der Funktion f an ihren Definitionsgrenzen, und geben
Sie die Gleichungen der Asymptoten ihres Grafen an.
10.3 Ermitteln Sie das Monotonie- und Krümmungsverhalten von f. Geben Sie auch die Art
und die Koordinaten eventueller Horizontal- und Flachpunkte an.
10.4 Zeichnen Sie den Grafen von f für x ≤ 10.
10.5 In einer Integral-Formelsammlung steht: 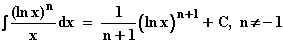 .
Bestätigen Sie diese Formel rechnerisch, und bestimmen Sie dann die Fläche, die der
Graf von f mit dem Grafen der Funktion g: x
.
Bestätigen Sie diese Formel rechnerisch, und bestimmen Sie dann die Fläche, die der
Graf von f mit dem Grafen der Funktion g: x 
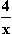 einschließt!
10.6 Die Tangente durch den Hochpunkt von Gf schneidet den Grafen von f noch in einem
zweiten Punkt. Ermitteln Sie die Abszisse dieses Punktes nach dem Newtonschen
Näherungsverfahren auf 2 Dezimalen genau!
10.7 Bestimmen Sie unter Beachtung der Aufgaben 10.5 und 10.6 die Fläche, die der Graf
von f mit der Tangente durch den Hochpunkt von Gf einschließt!
einschließt!
10.6 Die Tangente durch den Hochpunkt von Gf schneidet den Grafen von f noch in einem
zweiten Punkt. Ermitteln Sie die Abszisse dieses Punktes nach dem Newtonschen
Näherungsverfahren auf 2 Dezimalen genau!
10.7 Bestimmen Sie unter Beachtung der Aufgaben 10.5 und 10.6 die Fläche, die der Graf
von f mit der Tangente durch den Hochpunkt von Gf einschließt!
 11. Gegeben ist die Funktion f: x
11. Gegeben ist die Funktion f: x 
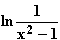 .
11.1 Diskutieren Sie f in Bezug auf den max. Definitionsbereich, Symmetrie, Verhalten an
den Rändern des Definitionsbereichs, Asymptoten, Nullstellen sowie das Monotonie-
und Krümmungsverhalten.
11.2 Zeichnen Sie den Grafen von f.
11.3 Die quadratische Funktion g(x) = ax
.
11.1 Diskutieren Sie f in Bezug auf den max. Definitionsbereich, Symmetrie, Verhalten an
den Rändern des Definitionsbereichs, Asymptoten, Nullstellen sowie das Monotonie-
und Krümmungsverhalten.
11.2 Zeichnen Sie den Grafen von f.
11.3 Die quadratische Funktion g(x) = ax + b soll die auf den Bereich |x| >
+ b soll die auf den Bereich |x| > 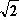 beschränkte
Funktion f zwischen x = –
beschränkte
Funktion f zwischen x = –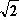 und x =
und x = 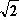 so ergänzen, dass die aus f und g zusammen-
gesetzte Funktion überall stetig und differnzierbar ist. Bestimmen Sie die Parameter a
und b!
so ergänzen, dass die aus f und g zusammen-
gesetzte Funktion überall stetig und differnzierbar ist. Bestimmen Sie die Parameter a
und b!
 12. Gegeben ist die Funktion f: x
12. Gegeben ist die Funktion f: x 
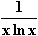 .
12.1 Diskutieren Sie f in Bezug auf den max. Definitionsbereich, Verhalten an den
Rändern des Definitionsbereichs, Asymptoten, Nullstellen sowie das Monotonie- und
Krümmungsverhalten.
12.2 Zeichnen Sie den Grafen von f.
12.3 Gegeben ist die Funktion g: x
.
12.1 Diskutieren Sie f in Bezug auf den max. Definitionsbereich, Verhalten an den
Rändern des Definitionsbereichs, Asymptoten, Nullstellen sowie das Monotonie- und
Krümmungsverhalten.
12.2 Zeichnen Sie den Grafen von f.
12.3 Gegeben ist die Funktion g: x 
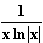 . Beschreiben Sie mit Hilfe bisheriger
Ergebnisse möglichst präzise den Verlauf des Grafen von g!
12.4 Bestimmen Sie die Gleichungen der drei den Grafen von f rechts vom Hochpunkt
berührenden Tangenten, die mit den Achsen jeweils eine Dreiecksfläche mit der
Maßzahl 2,25 einschließen!
. Beschreiben Sie mit Hilfe bisheriger
Ergebnisse möglichst präzise den Verlauf des Grafen von g!
12.4 Bestimmen Sie die Gleichungen der drei den Grafen von f rechts vom Hochpunkt
berührenden Tangenten, die mit den Achsen jeweils eine Dreiecksfläche mit der
Maßzahl 2,25 einschließen!
 13. (BOS-Abschlussprüfung 2000, Nachschreibtermin)
Für den Zusammenhang zwischen der Reizgröße R und der Empfindung E gelte das
Weber-Fechnersche Gesetz: E = K + c ln(R). Dabei sind K und c positive reelle Zahlen.
13.1 Für R=2 erhält man E=4 und für R=5 ergibt sich E=6. Berechnen Sie die Konstanten K
und c. (Zur Kontrolle: c ≈ 2,183; K ≈ 2,487)
13.2 In einem Versuch darf man das Empfindungsmaximum Emax=10 nicht überschreiten.
Berechnen Sie das hierzu gehörige Reizmaximum.
13.3 Zeigen Sie: Jede Halbierung der Reizgröße vermindert die Empfindung um ca. 1,5
Einheiten. Was bewirkt eine Verzehnfachung des Reizes?
13. (BOS-Abschlussprüfung 2000, Nachschreibtermin)
Für den Zusammenhang zwischen der Reizgröße R und der Empfindung E gelte das
Weber-Fechnersche Gesetz: E = K + c ln(R). Dabei sind K und c positive reelle Zahlen.
13.1 Für R=2 erhält man E=4 und für R=5 ergibt sich E=6. Berechnen Sie die Konstanten K
und c. (Zur Kontrolle: c ≈ 2,183; K ≈ 2,487)
13.2 In einem Versuch darf man das Empfindungsmaximum Emax=10 nicht überschreiten.
Berechnen Sie das hierzu gehörige Reizmaximum.
13.3 Zeigen Sie: Jede Halbierung der Reizgröße vermindert die Empfindung um ca. 1,5
Einheiten. Was bewirkt eine Verzehnfachung des Reizes?
 14. Ein Volumenteil einer Säure vom pH-Wert 1 wird mit
a) 9 Volumenteilen; b) 4 Volumenteilen reinen Wassers verdünnt.
Welchen pH-Wert hat jeweils die so entstehende verdünnte Säure?
14. Ein Volumenteil einer Säure vom pH-Wert 1 wird mit
a) 9 Volumenteilen; b) 4 Volumenteilen reinen Wassers verdünnt.
Welchen pH-Wert hat jeweils die so entstehende verdünnte Säure?
 15. Ein Volumenteil einer Säure vom pH-Wert 1 wird mit reinem Wasser so verdünnt, dass die entstehende
verdünnte Säure den pH-Wert
a) 3; b) 3,699 besitzt.
Wie viele Volumenteile Wasser sind zur genannten Verdünnung jeweils notwendig?
15. Ein Volumenteil einer Säure vom pH-Wert 1 wird mit reinem Wasser so verdünnt, dass die entstehende
verdünnte Säure den pH-Wert
a) 3; b) 3,699 besitzt.
Wie viele Volumenteile Wasser sind zur genannten Verdünnung jeweils notwendig?

 – 1) ln(x
– 1) ln(x – 4)
– 4)  – 4) ln(x
– 4) ln(x – 1)
– 1)  ln(x
ln(x + 1)
+ 1)
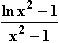
 )
)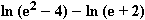
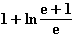
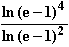
 ln (4 – 2x)
ln (4 – 2x) b) f: x
b) f: x  ln (2 – x)(1 + x) c) f: x
ln (2 – x)(1 + x) c) f: x  ln
ln 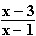
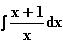 b)
b) 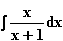 c)
c) 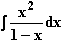 d)
d) 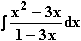

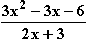 mit max. Definitionsmenge.
mit max. Definitionsmenge.
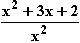 mit max. Definitionsmenge.
mit max. Definitionsmenge. x (ln x – 1).
x (ln x – 1).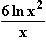 .
9.1 Diskutieren Sie f in Bezug auf den max. Definitionsbereich, Symmetrie, Verhalten an
den Rändern des Definitionsbereichs, Asymptoten, Nullstellen sowie Extrem- und
Wendepunkte.
9.2 Zeichnen Sie den Grafen von f.
9.3 Aus der Funktion f soll eine abschnittsweise definierte Funktion g gewonnen werden,
die die Polstelle von f „überbrückt“. Dazu soll diejenige Gerade aus der Schar y = mx,
die die Äste des Grafen von f berührt, zwischen den Berührpunkten den Grafen von f
ersetzen. Ermitteln Sie diese Gerade, und geben Sie die Funktionsgleichung der
Funktion g an!
.
9.1 Diskutieren Sie f in Bezug auf den max. Definitionsbereich, Symmetrie, Verhalten an
den Rändern des Definitionsbereichs, Asymptoten, Nullstellen sowie Extrem- und
Wendepunkte.
9.2 Zeichnen Sie den Grafen von f.
9.3 Aus der Funktion f soll eine abschnittsweise definierte Funktion g gewonnen werden,
die die Polstelle von f „überbrückt“. Dazu soll diejenige Gerade aus der Schar y = mx,
die die Äste des Grafen von f berührt, zwischen den Berührpunkten den Grafen von f
ersetzen. Ermitteln Sie diese Gerade, und geben Sie die Funktionsgleichung der
Funktion g an!
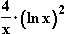 .
10.1 Geben Sie den maximalen Definitionsbereich von f an!
10.2 Untersuchen Sie das Verhalten der Funktion f an ihren Definitionsgrenzen, und geben
Sie die Gleichungen der Asymptoten ihres Grafen an.
10.3 Ermitteln Sie das Monotonie- und Krümmungsverhalten von f. Geben Sie auch die Art
und die Koordinaten eventueller Horizontal- und Flachpunkte an.
10.4 Zeichnen Sie den Grafen von f für x ≤ 10.
10.5 In einer Integral-Formelsammlung steht:
.
10.1 Geben Sie den maximalen Definitionsbereich von f an!
10.2 Untersuchen Sie das Verhalten der Funktion f an ihren Definitionsgrenzen, und geben
Sie die Gleichungen der Asymptoten ihres Grafen an.
10.3 Ermitteln Sie das Monotonie- und Krümmungsverhalten von f. Geben Sie auch die Art
und die Koordinaten eventueller Horizontal- und Flachpunkte an.
10.4 Zeichnen Sie den Grafen von f für x ≤ 10.
10.5 In einer Integral-Formelsammlung steht: 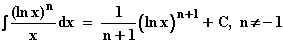 .
Bestätigen Sie diese Formel rechnerisch, und bestimmen Sie dann die Fläche, die der
Graf von f mit dem Grafen der Funktion g: x
.
Bestätigen Sie diese Formel rechnerisch, und bestimmen Sie dann die Fläche, die der
Graf von f mit dem Grafen der Funktion g: x 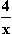 einschließt!
10.6 Die Tangente durch den Hochpunkt von Gf schneidet den Grafen von f noch in einem
zweiten Punkt. Ermitteln Sie die Abszisse dieses Punktes nach dem Newtonschen
Näherungsverfahren auf 2 Dezimalen genau!
10.7 Bestimmen Sie unter Beachtung der Aufgaben 10.5 und 10.6 die Fläche, die der Graf
von f mit der Tangente durch den Hochpunkt von Gf einschließt!
einschließt!
10.6 Die Tangente durch den Hochpunkt von Gf schneidet den Grafen von f noch in einem
zweiten Punkt. Ermitteln Sie die Abszisse dieses Punktes nach dem Newtonschen
Näherungsverfahren auf 2 Dezimalen genau!
10.7 Bestimmen Sie unter Beachtung der Aufgaben 10.5 und 10.6 die Fläche, die der Graf
von f mit der Tangente durch den Hochpunkt von Gf einschließt!
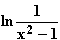 .
11.1 Diskutieren Sie f in Bezug auf den max. Definitionsbereich, Symmetrie, Verhalten an
den Rändern des Definitionsbereichs, Asymptoten, Nullstellen sowie das Monotonie-
und Krümmungsverhalten.
11.2 Zeichnen Sie den Grafen von f.
11.3 Die quadratische Funktion g(x) = ax
.
11.1 Diskutieren Sie f in Bezug auf den max. Definitionsbereich, Symmetrie, Verhalten an
den Rändern des Definitionsbereichs, Asymptoten, Nullstellen sowie das Monotonie-
und Krümmungsverhalten.
11.2 Zeichnen Sie den Grafen von f.
11.3 Die quadratische Funktion g(x) = ax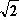 beschränkte
Funktion f zwischen x = –
beschränkte
Funktion f zwischen x = –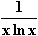 .
12.1 Diskutieren Sie f in Bezug auf den max. Definitionsbereich, Verhalten an den
Rändern des Definitionsbereichs, Asymptoten, Nullstellen sowie das Monotonie- und
Krümmungsverhalten.
12.2 Zeichnen Sie den Grafen von f.
12.3 Gegeben ist die Funktion g: x
.
12.1 Diskutieren Sie f in Bezug auf den max. Definitionsbereich, Verhalten an den
Rändern des Definitionsbereichs, Asymptoten, Nullstellen sowie das Monotonie- und
Krümmungsverhalten.
12.2 Zeichnen Sie den Grafen von f.
12.3 Gegeben ist die Funktion g: x 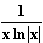 . Beschreiben Sie mit Hilfe bisheriger
Ergebnisse möglichst präzise den Verlauf des Grafen von g!
12.4 Bestimmen Sie die Gleichungen der drei den Grafen von f rechts vom Hochpunkt
berührenden Tangenten, die mit den Achsen jeweils eine Dreiecksfläche mit der
Maßzahl 2,25 einschließen!
. Beschreiben Sie mit Hilfe bisheriger
Ergebnisse möglichst präzise den Verlauf des Grafen von g!
12.4 Bestimmen Sie die Gleichungen der drei den Grafen von f rechts vom Hochpunkt
berührenden Tangenten, die mit den Achsen jeweils eine Dreiecksfläche mit der
Maßzahl 2,25 einschließen!