Bestimmung eines allgemeinen Dreiecks |
| |
|
|
|
|
|
| |
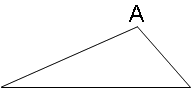
Beschriften sie die folgenden Dreiecke vollständig. |
|
| |
| 1. |
 |
|
 
|
| |
|
|
| |
| 2. |
 |
|
|
| |
|
|
| |
| 3. |
 |
|
|
|
|
|
| |
|
|
|
|
| |
|
|
| |
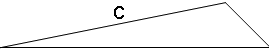| 1. |
Die Seiten eines Dreiecks haben die Längen 2 cm, 7cm und 25 cm.
Berechnen sie den Umfang. |
|
|
| |
|
|
| |
| 2. |
Der Umfang eines Dreiecks beträgt 2,5 dm und dessen Seiten a = 8 cm und b = 10 cm.
Berechnen sie die Seite c. |
|
|
| |
|
|
| |
| 3. |
Der Umfang eines Dreiecks beträgt 36 cm. Berechnen sie die Länge der Seite a,
wenn diese doppelt so lang ist, wie b. Die Seite b ist 3 mal so groß, wie die Seite c. |
|
|
| |
|
|
| |
| 4. |
Die Grundlinie g eines Dreiecks ist 25 cm lang und die Höhe h 18 cm.
Berechnen sie die Fläche. |
|
|
| |
|
|
| |
| 5. |
64 cm² = ½ • g • 17,5 cm; Berechnen sie g.
|
|
|
| |
|
|
| |
| 6. |
Der Umfang eines Dreiecks beträgt 89 cm, die Seite a = 11 cm und b = 13 cm.
Berechne c und den entsprechenden Flächeninhalt,
wenn die Höhe über c gleich 7 cm ist. |
|
|
| |
|
|
|
|
|
| |
|
|
| Typen der Dreiecke |
| |
|
|
| |
Bezeichnen sie die folgenden Dreiecke nach ihren Typen. |
|
| |
|
|
|
|
|
| |
|
|
| |
|
|
| Besondere Dreiecke |
| |
|
|
- gleichschenkliges Dreieck
|
|
| |
|
|
| |
| 1. |
Ein gleichschenkliges Dreieck hat den Umfang von 32 cm.
Berechnen sie die Schenkel a und b, wenn die Basis 12 cm beträgt. |
|
|
| |
|
|
| |
| 2. |
In einem gleichschenkigen Dreieck beträgt der Winkel α, zwischen Basis und Schenkel, 40°.
Berechnen sie die fehlenden Winkel. |
|
|
| |
|
|
|
| 3. |
In einem gleichschenkligen Dreieck beträgt
der Winkel δ zwischen dem Lot über der Basis
und dem Schenkel 15°.
Berechnen sie die fehlenden Winkel. |
|
|
| |
|
|
| |
|
|
|
| |
|
|
| |
| 1. |
Die Seite a eines gleichseitigen Dreiecks beträgt 13 cm.
Berechnen sie die Fläche. |
|
|
| |
|
|
| |
| 2. |
Die Fläche eines gleichseitigen Dreiecks beträgt 43 cm².
Berechnen sie die Seite a. |
|
|
| |
|
|
| |
| 3. |
Die Höhe eines gleichseitigen Dreiecks beträgt 17cm.
Berechnen sie die Fläche. |
|
|
| |
|
|
|
|
|
|
| |
|
|
| |
PYTHAGORAS: |
|
| |
| 1. |
In einem rechtwinkligen Deieck ist a =
3 cm und b = 4 cm.
Berechnen sie c. |
|
|
| |
|
|
| |
| 2. |
In einem rechtwinkligen Dreieck ist a = 25 cm und c = 80 cm.
Berechnen sie b. |
|
|
| |
|
|
| |
| 3. |
In einem gleichschenkligen Dreieck ist die Höhe über der Basis 12 cm und ein
Schenkel 18 cm. Berechnen sie die Länge der Basis.
|
|
|
| |
|
|
| |
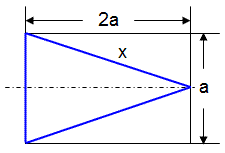
| 4. |
Berechnen sie die Größe x, die Fläche A und den Umfang U der blau umrahmten
Teilfäche in Abhängigkeit von der Größe a.
|
|
|
| |
|
|
| |
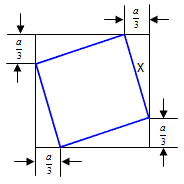
| 5. |
Berechnen sie die Größe x, die Fläche A und den Umfang U der blau umrahmten
Teilfäche in Abhängigkeit von der gegebenen
Göße a der Quadratseite.
|
|
|
|
|
|
| |
|
|
| |
KATHETENSATZ: |
|
| |
| 1. |
Berechnen sie die Seite a, wenn c = 11 und q = 8,5.
|
|
|
|
| |
|
|
| |
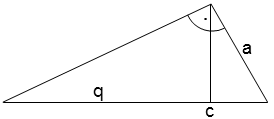
| 2. |
Gegeben sind bei einem rechtwinkligen Dreieck:
U = 36 mm; a = 9 mm; b = 12 mm;
Berechnen sie die Hypotenuse c und den Hypotenusenabschnitt q. |
|
|
| |
|
|
| |
| 3. |
Bei einem rechtwinkligen Dreieck ist die Hypotenuse
c = 20 cm und dessen Hypotenusenabschnitt p = 16 cm
lang.
Berechnen sie die Seiten a und b, sowie den Umfang.
|
|
|
| |
|
|
|
|
|
| |
HÖHENSATZ: |
|
| |
| 1. |
Die Höhe eines rechtwinkligen Dreiecks ist 12 cm.
Welche ganzzahligen Werte können p und q annehmen? |
|
|
| |
|
|
| |
| 2. |
Die Höhe eines rechtwinkligen Dreiecks ist 5,2 cm und der Hypotenusenabschnitt q ist 4,5 cm.
Berechnen sie die Seiten a, b und c. |
|
|
| |
|
|
| |
|
|
| |
|
|
|
Erklärungen |
 Aufgaben 1 |
 Aufgaben 2 |
 Lösungen |
|
| |
|
|
| |
|
|
