• Eigenschaften und Definition
• Bernoulli-Experiment
• Erwartungswert
• Varianz und Standardabweichung
• Kumulative Verteilungsfunktion
• Histogramme
• Übungsblatt

1. Eigenschaften und Definition:

Die Binomialverteilung dient der Beschreibung von sehr unterschiedlichen statistischen Problemen, die alle folgende einheitliche Struktur haben:

( I ) : Es liegt ein Zufallsexperiment zugrunde, bei dem nur zwei Ergebnisse und unterschieden werden. Solch ein Zufallsexperiment wird auch Bernoulli- Experiment genannt (siehe 2.)

Beispiele:

• In der Qualitätskontrolle werden bei der Entnahme von Produkten aus der Produktion z. B. die beiden Ereignisse "fehlerhaft" und "fehlerfrei" unterschieden.
• In der Geburtenstatistik gilt das Interesse einer Statistik der beiden Ergebnisse "Mädchen" und "Junge"
• Bei einem Würfelspiel interessiert man sich für die beiden Ergebnisse "sechs" und "nicht sechs"

( II ): Das Zufallsexperiment wird n-mal wiederholt. Die Wahrscheinlichkeiten beider Ausgänge sind bei jeder Wiederholung identisch.

Beispiele:

• In der Qualitätskontrolle entnimmt und prüft man mehrere Produkte aus der Produktion.
• Man registriert die Ergebnisse einer Vielzahl von Geburten.
• Man würfelt mehrmals

( III ): Man interessiert sich für die Wahrscheinlichkeit dafür, dass bei n-maliger Durchführung des Zufallsexperiment das Ereignis A genau bzw. höchstens bzw. mindestens k-mal eintrifft (siehe 5.).

Beispiele:

• Man interessiert sich für die Wahrscheinlichkeit dafür, dass bei der Entnahme von zehn Produkten höchstens drei fehlerhaft sind.
• Man interessiert sich für die Wahrscheinlichkeit dafür, dass unter zehn Geburten genau fünf Jungen sind.
• Man interessiert sich für die Wahrscheinlichkeit dafür, dass bei 10-maligem Würfeln mindestens einmal sechs aufgetreten ist.

1.2 Definition

Nimmt eine Zufallsgröße X die Werte 1, 2 bis n mit den Wahrscheinlichkeiten
P (X = k) = B (n; p; k) = * p^k * (1-p) ^n-k für alle k {1, 2, ..., n} an,
so heißt X binomialverteilt mit den Parametern n und p oder kürzer B (n; p)-verteilt. Die zugehörige Wahrscheinlichkeitsverteilung heißt Binomialverteilung mit den Parametern n und p.

Von besonderer Bedeutung sind Zufallsexperimente mit genau zwei möglichen Ergebnissen wie zum Beispiel:

• Treffer, Niete
• Kopf, Zahl
• positiv, negativ
• bestanden, nicht bestanden
  

Diese Experimente gehen zurück auf den Mathematiker Jacob Bernoulli und werden deshalb Bernoulli-Experimente genannt. Als bekanntestes Beispiel dient wohl der Münzwurf. Eine n-fache Wiederholung eines solchen Bernoulli-Experiments nennt man auch Bernoulli-Kette der Länge n.
Die Trefferwahrscheinlichkeit p des Bernoulli-Experiments, die sich natürlich nicht verändert, bezeichnet man auch als Trefferwahrscheinlichkeit der Bernoulli-Kette.

2.1 Einführungsbeispiel:

Aus einer Urne mit zehn Kugeln, drei schwarze und sieben weiße, werden drei Kugeln mit zurücklegen gezogen.

Frage: Wie viele Möglichkeiten gibt es genau zwei schwarze Kugeln zu ziehen?

Frage: Wie groß ist die Wahrscheinlichkeit genau zwei schwarze Kugeln zu ziehen?

2.2 Lösungsformel (Bernoulli-Formel):

Ersetzen wir also, wie im Einführungsbeispiel gesehen, die Länge der Bernoulli-Kette drei durch n, die Trefferzahl zwei durch k und die Trefferwahrscheinlichkeit 0,3 durch p, so ergibt sich folgende Formel:

Die Wahrscheinlichkeit für genau k Treffer bei einer Bernoulli-Kette der Länge n mit der Trefferwahrscheinlichkeit p beträgt

* p^k * (1-p)^n-k
und wird mit B (n; p; k) bezeichnet. Es gilt also

B (n; p; k) = * pk * (1-p)n-k

B (n; p) ist der Name für die Wahrscheinlichkeitsverteilung, während
B (n; p; k) den einzelnen Wert der Wahrscheinlichkeit angibt.

Fassen wir noch mal zusammen:

Die Anzahl der durchgeführten gleichen Bernoulli-Experimente nennt man auch Bernoulli-Kette der Länge n. Sei nun die Trefferwahrscheinlichkeit des einzelnen Bernoulli-Experiments P ({Treffer}) = p, die Nietenwahrscheinlichkeit P ({Niete}) = q = 1 - p. Die Lösungsformel gibt Auskunft über die Wahrscheinlichkeit B (n; p; k), in einer Bernoulli-Kette der Länge n und der Trefferwahrscheinlichkeit p genau k Treffer zu erhalten.

Die Bernoulli-Formel gilt eigentlich nur für Experimente "Ziehen mit zurücklegen", bei denen sich die Trefferwahrscheinlichkeit p nicht verändert. Sie wird aber auch für Experimente "Ziehen ohne zurücklegen" angewendet, wenn sich dabei die Trefferwahrscheinlichkeit p praktisch nicht verändert. Dies ist beispielsweise bei Massenproduktionen der Fall.

Beispiel 2.2.1:
Eine Mannschaft gewinnt ihre Spiele mit einer Wahrscheinlichkeit von . Mit welcher Wahrscheinlichkeit gewinnt die Mannschaft genau zwei der nächsten fünf Spiele?

3. Der Erwartungswert:

Der Erwartungswert ( µ ) einer binomialverteilten Zufallsgröße errechnet sich wie folgt:

Beispiel 3.1:
20 % einer Lieferung Fliesen seien Ausschuss. Wie viele Fehlstücke sind unter 50 Fliesen im Mittel zu erwarten, wenn sie einer Massenproduktion zufällig entnommen werden?

Beispiel 3.2:
Auf einem Eisenbahnnetz, das von einem Bahnkraftwerk mit Strom versorgt wird, verkehren zehn Lokomotiven. Die Wahrscheinlichkeit, dass in einer bestimmten Zeit eine Lokomotive anfährt und eine Stromeinheit verbraucht, sei gleich 0,2 für jede Lok. Mit welchem mittleren Strombedarf ist zu rechnen?

4. Varianz und Standardabweichung

4.1 Varianz

Die Varianz einer binomialverteilten Zufallsgröße X berechnet sich wie folgt (ohne Nachweis):

Frage: wie lautet die Varianz von Beispiel 3.1?

4.2 Standardabweichung

Wie bereits bekannt, (siehe Kapitel Zufallsgrößen) berechnet sich somit die Standardabweichung, indem man die Wurzel aus der Varianz zieht:

Frage: Wie lautet die Standardabweichung von Beispiel 3.1?

  5. Kumulative Verteilungsfunktion

Die Frage ist nun: Mit welcher Wahrscheinlichkeit haben wir höchstens k Erfolge auf n Versuche?
Für die Werte der (kumulativen) Verteilungsfunktion F einer binomialverteilten Zufallsgröße X gilt:

F (k) = P (X 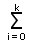k) = B (n; p; i)

Statt F (k) schreibt man häufig auch (k), also (k) = B (n; p; i),
d. h. bei dieser Schreibweise wird die Anzahl n der Durchführungen des Zufallsexperiments mit der Trefferwahrscheinlichkeit p verdeutlicht.

Es sei nun bekannt, dass von einer bestimmten Sorte von Tulpenzwiebeln 10 % nicht keimen.

Beispiel "genau k Treffer":
Mit welcher Wahrscheinlichkeit enthält eine Packung von 25 zufällig ausgewählten Zwiebeln genau drei Zwiebeln, die nicht aufgehen?


Beispiel "höchstens k Treffer":
Mit welcher Wahrscheinlichkeit sind höchstens drei Zwiebeln, die nicht aufgehen, in einer Packung von 25 zufällig ausgewählten Zwiebeln enthalten?


Beispiel "mehr als k Treffer":
Mit welcher Wahrscheinlichkeit sind mehr als fünf Zwiebeln, die nicht aufgehen, in einer Packung von 25 zufällig ausgewählten Zwiebeln enthalten?


Beispiel "mindestens k und höchstens m Treffer":
Mit welcher Wahrscheinlichkeit sind mindestens zwei und höchstens vier Zwiebeln, die nicht aufgehen, in einer Packung aus 25 zufällig ausgewählten Zwiebeln enthalten?

Beispiel "mindestens k Treffer":
Mit welcher Wahrscheinlichkeit sind mindestens 8 Zwiebeln, die nicht aufgehen, in einer Packung aus 25 zufällig ausgewählten Zwiebeln?

top