Übungsblatt Leontief-Modell
OStR Litzberski
Aufgabe 1
In den 3 Zweigwerken Z1, Z2 und Z3 eines großen Betriebes wird jeweils für die beiden anderen
Zweigwerke und für den Eigenverbrauch produziert. Die folgende Tabelle gibt die Produktionszahlen
in Mengeneinheiten ( ME ) an. Sie beziehen sich auf 1 Produktionsperiode.
Die gegenseitige Abhängigkeit der Zweigwerke wird durch das Leontief-Modell beschrieben.
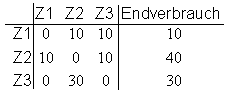 a) Berechnen Sie die Inputmatrix nach dem Leontief-Modell.
b) Wieviele Mengeneinheiten stehen für den Endverbrauch zur Verfügung,
wenn im 1. Zweigwerk 100 ME, im 2. Zweigwerk 180 ME und
im 3. Zweigwerk 120 ME produziert werden?
c) In der nächsten Produktionsperiode benötigt man für den Endverbrauch 60 ME vom
Werk Z1, 75 ME vom Werk Z2 und 90 ME vom Werk Z3.
Berechnen Sie, wieviele ME dann in den einzelnen Zweigwerken produziert werden müssen.
a) Berechnen Sie die Inputmatrix nach dem Leontief-Modell.
b) Wieviele Mengeneinheiten stehen für den Endverbrauch zur Verfügung,
wenn im 1. Zweigwerk 100 ME, im 2. Zweigwerk 180 ME und
im 3. Zweigwerk 120 ME produziert werden?
c) In der nächsten Produktionsperiode benötigt man für den Endverbrauch 60 ME vom
Werk Z1, 75 ME vom Werk Z2 und 90 ME vom Werk Z3.
Berechnen Sie, wieviele ME dann in den einzelnen Zweigwerken produziert werden müssen.
Aufgabe 2
Für die 3 Sektoren S1, S2 und S3 einer Volkswirtschaft legt man das Modell von Leontief zugrunde.
Die Gesamtproduktion von S1 beträgt 30 Einheiten, von S2 40 Einheiten und von S3 ebenfalls
40 Einheiten. Die gegenseitige Verflechtung in der laufenden Produktionsperiode wird durch das
folgende Diagramm beschrieben :
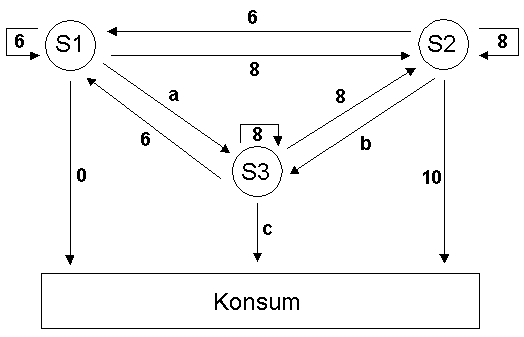 a) Berechnen Sie die Werte von a, b und c und stellen Sie die gegenseitige Verfechtung der
Sektoren in einer Tabelle dar.
b) Welcher Konsumvektor ergibt sich bei einem Produktionsvektor ( 40 50 30 )T ?
c) Wieviele Einheiten müssen die Sektoren in einer Periode produzieren, wenn der
Konsumvektor ( 18 24 12 )T beträgt ?
a) Berechnen Sie die Werte von a, b und c und stellen Sie die gegenseitige Verfechtung der
Sektoren in einer Tabelle dar.
b) Welcher Konsumvektor ergibt sich bei einem Produktionsvektor ( 40 50 30 )T ?
c) Wieviele Einheiten müssen die Sektoren in einer Periode produzieren, wenn der
Konsumvektor ( 18 24 12 )T beträgt ?
Aufgabe 3
Drei Sektoren A, B und C eines Unternehmens sind so miteinander verflochten, dass man
sie mit dem Modell von Leontief beschreiben kann. Die folgende Tabelle gibt an, welche
Mengeneinheiten in der vergangenen Produktionsperiode produziert und geliefert wurden.
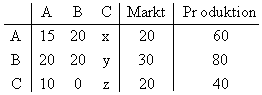 a) Berechnen Sie, welche Mengeneinheiten an den Sektor C geliefert wurden und bestimmen
Sie die Inputmatrix, die zu dieser Verflechtung gehört.
b) Die Nachfrage nach den Produkten der Sektoren A und B steigt, während die Nachfrage nach den
Produkten des Sektors C unverändert bleibt. Man beschließt daher, die Produktion des
Sektors A um 20 % und die Produktion von B um 40 % zu steigern.
Wieviele Mengeneinheiten mehr müssen dann im Sektor C produziert werden?
c) Für die nächste Produktionsperiode rechnet man mit einer geänderten Nachfrage.
Man geht davon aus, dass von den Produkten des Sektors A 24 Einheiten,
von Sektor B 20 Einheiten und von C 16 Einheiten nachgefragt werden.
Wieviel wird dann in den einzelnen Sektoren produziert werden, wenn man sich an diese neue
Situation anpasst?
a) Berechnen Sie, welche Mengeneinheiten an den Sektor C geliefert wurden und bestimmen
Sie die Inputmatrix, die zu dieser Verflechtung gehört.
b) Die Nachfrage nach den Produkten der Sektoren A und B steigt, während die Nachfrage nach den
Produkten des Sektors C unverändert bleibt. Man beschließt daher, die Produktion des
Sektors A um 20 % und die Produktion von B um 40 % zu steigern.
Wieviele Mengeneinheiten mehr müssen dann im Sektor C produziert werden?
c) Für die nächste Produktionsperiode rechnet man mit einer geänderten Nachfrage.
Man geht davon aus, dass von den Produkten des Sektors A 24 Einheiten,
von Sektor B 20 Einheiten und von C 16 Einheiten nachgefragt werden.
Wieviel wird dann in den einzelnen Sektoren produziert werden, wenn man sich an diese neue
Situation anpasst?
Aufgabe 4
Drei Sektoren A, B und C einer Volkswirtschaft tauschen entsprechend der folgenden Tabelle
untereinander Waren aus und beliefern den Markt. Die Zahlen beziehen sich auf Mengeneinheiten
in der laufenden Produktionsperiode. Man geht davon aus, dass die Sektoren nach dem
Leontief-Modell miteinander verknüpft sind.
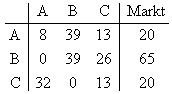 a) Bestimmen Sie die Inputmatrix.
a) Bestimmen Sie die Inputmatrix.
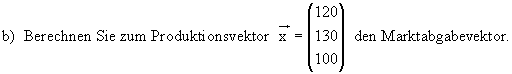
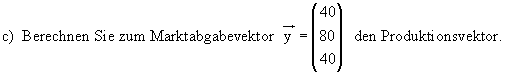 d) Für den kommenden Produktionszeitraum erwartet man, dass sich die Nachfrage nach
den Gütern von B und C nicht ändert, aber die Nacgfrage nach den Gütern von A steigt.
Man beschließt daher, die Produktion im Sektor A um 70 ME zu erhöhen.
( Die Angaben beziehen sich auf die anfangs gegebene Tabelle, nicht auf die Aufgabe b und c.)
Um wieviele ME steigt dann auch die Produktion in den Sektoren B und C ?
d) Für den kommenden Produktionszeitraum erwartet man, dass sich die Nachfrage nach
den Gütern von B und C nicht ändert, aber die Nacgfrage nach den Gütern von A steigt.
Man beschließt daher, die Produktion im Sektor A um 70 ME zu erhöhen.
( Die Angaben beziehen sich auf die anfangs gegebene Tabelle, nicht auf die Aufgabe b und c.)
Um wieviele ME steigt dann auch die Produktion in den Sektoren B und C ?
Aufgabe 5
Drei Sektoren S1, S2 und S3 einer Volkswirtschaft sind nach dem Leontief-Modell
miteinander verknüpft. Die gegenseitigen Lieferungen während einer Produktionsperiode
in Mengeneinheiten ( ME ), die Abgabe an den Markt und die Gesamtproduktion sind der folgenden
Tabelle zu entnehmen :
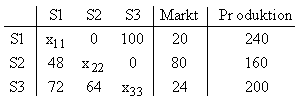 a) Bestimmen Sie die Inputmatrix, die zu dieser Verflechtung gehört.
b) Wie groß muss die Produktion in jedem der Sektoren sein, wenn eine Marktabgabe
a) Bestimmen Sie die Inputmatrix, die zu dieser Verflechtung gehört.
b) Wie groß muss die Produktion in jedem der Sektoren sein, wenn eine Marktabgabe
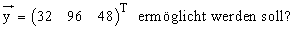
 d) Für die nächste Periode plant man in S1 eine Produktion von 300 ME,
in S2 von 220 ME. Jeder Sektor soll so viel produzieren, dass von den Gütern jedes
Sektors mindestens 20 ME an den Markt abgegeben werden können.
Wieviele ME muss man dann in S3 mindestens, höchstens produzieren?
e) Im folgenden hängt der Produktionsvektor von einer positiven Variablen a ab.
d) Für die nächste Periode plant man in S1 eine Produktion von 300 ME,
in S2 von 220 ME. Jeder Sektor soll so viel produzieren, dass von den Gütern jedes
Sektors mindestens 20 ME an den Markt abgegeben werden können.
Wieviele ME muss man dann in S3 mindestens, höchstens produzieren?
e) Im folgenden hängt der Produktionsvektor von einer positiven Variablen a ab.
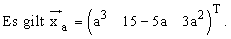 Beim Verkauf erzielt man bei den Gütern von S1 und S3 jeweils 15 GE ( Geldeinheiten ),
bei S2 30 GE pro Mengeneinheit.
Bei welchem Wert von a nehmen die Gesamteinnahmen ein relatives Maximum an ?
Beim Verkauf erzielt man bei den Gütern von S1 und S3 jeweils 15 GE ( Geldeinheiten ),
bei S2 30 GE pro Mengeneinheit.
Bei welchem Wert von a nehmen die Gesamteinnahmen ein relatives Maximum an ?
Aufgabe 6
Drei Zweigwerke Z1, Z2 und Z3 eines großen Betriebes sind nach dem Leontief-Modell
miteinander verknüpft. Das Diagramm gibt an, welche Mengeneinheiten in einem bestimmten
Produktionszeitraum zwischen den Zweigwerken ausgetauscht werden und welche Mengen an den
Markt abgegeben werden.
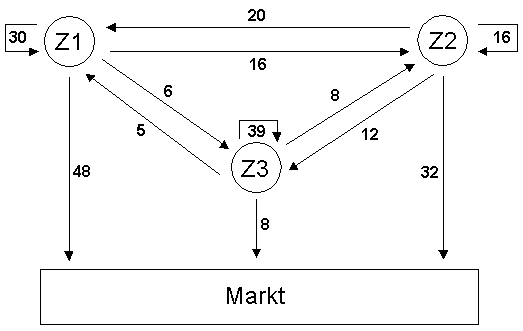
 Wieviele Mengeneinheiten werden dann von den Zweigwerken an den Markt abgegeben?
b) Berechnen Sie den Marktabgabe- und den Produktionsvektor für den Fall, dass alle
Zweigwerke gleich viel an den Markt abgeben und im 3. Zweigwerk 66 Menheneinheiten
produziert werden.
Wieviele Mengeneinheiten werden dann von den Zweigwerken an den Markt abgegeben?
b) Berechnen Sie den Marktabgabe- und den Produktionsvektor für den Fall, dass alle
Zweigwerke gleich viel an den Markt abgeben und im 3. Zweigwerk 66 Menheneinheiten
produziert werden.
Aufgabe 7
Die Verflechtung dreier Sektoren A, B und C einer Volkswirtschaft soll dem Leontief-Modell genügen.
Sie wird durch folgende Inputmatrix beschrieben :
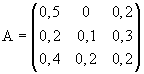 a) In der vergangenen Produktionsperiode stellte Sektor A insgesamt 400 Mengeneinheiten ( ME ) her,
Sektor B 600 ME und Sektor C 500 ME. Geben Sie in einer Tabelle an, wieviele Mengeneinheiten
die Sektoren untereinander austauschten und an den Konsum abgaben.
b) In der laufenden Produktionsperiode rechnet man mit einer Nachfrage von 125 ME nach den
Gütern von A, 300 ME nach den Gütern von B und 150 ME nach den Gütern von C.
Bestimmen Sie die entsprechenden Produktionsmengen in den einzelnen Sektoren.
a) In der vergangenen Produktionsperiode stellte Sektor A insgesamt 400 Mengeneinheiten ( ME ) her,
Sektor B 600 ME und Sektor C 500 ME. Geben Sie in einer Tabelle an, wieviele Mengeneinheiten
die Sektoren untereinander austauschten und an den Konsum abgaben.
b) In der laufenden Produktionsperiode rechnet man mit einer Nachfrage von 125 ME nach den
Gütern von A, 300 ME nach den Gütern von B und 150 ME nach den Gütern von C.
Bestimmen Sie die entsprechenden Produktionsmengen in den einzelnen Sektoren.
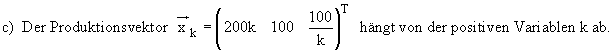 Für welche Werte von k (auf 2 Dezimalen) ist die Marktabgabe von B größer als
die Marktabgabe von Sektor A ?
d) Für die nächste Produktionsperiode hat man vor, die Fertigung umzustellen.
Dadurch ändern sich die Koeffizienten a13 und a23 der Inputmatrix.
Die Gesamtproduktionen der Sektoren A, B und C verhalten sich dann wie 5:3:4 .
Berechnen Sie die neue Inputmatrix und den neuen Produktionsvektor für einen
Für welche Werte von k (auf 2 Dezimalen) ist die Marktabgabe von B größer als
die Marktabgabe von Sektor A ?
d) Für die nächste Produktionsperiode hat man vor, die Fertigung umzustellen.
Dadurch ändern sich die Koeffizienten a13 und a23 der Inputmatrix.
Die Gesamtproduktionen der Sektoren A, B und C verhalten sich dann wie 5:3:4 .
Berechnen Sie die neue Inputmatrix und den neuen Produktionsvektor für einen
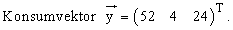
Aufgabe 8
(aus Abi 1999)
Drei Wirtschaftssektoren R, S und T sind nach dem Leontiefmodell miteinander und mit dem
Markt verbunden. Gegeben ist die Inputmatrix
 1. Erstellen Sie die zugehörige Input-Output-Tabelle, die auch den Konsumvektor erhält.
2. Die Produktion des Sektors R soll um a Einheiten erniedrigt werden, während die
Produktionseinheiten bei S und T konstant bleiben sollen.
Bestimmen Sie den maximal möglichen Wert von a .
3. Durch eine Umorganisation in Sektor T wurde erreicht, dass sich der Koeffizient a33 verändert.
Dadurch ergibt sich für den Produktionsvektor aus obiger Angabe,
dass von Sektor T 7 Einheiten auf den Markt kommen.
Ermitteln Sie die Marktabgaben von R und S sowie den Koeffizienten a33 ,
und erläutern Sie kurz dessen Bedeutung.
1. Erstellen Sie die zugehörige Input-Output-Tabelle, die auch den Konsumvektor erhält.
2. Die Produktion des Sektors R soll um a Einheiten erniedrigt werden, während die
Produktionseinheiten bei S und T konstant bleiben sollen.
Bestimmen Sie den maximal möglichen Wert von a .
3. Durch eine Umorganisation in Sektor T wurde erreicht, dass sich der Koeffizient a33 verändert.
Dadurch ergibt sich für den Produktionsvektor aus obiger Angabe,
dass von Sektor T 7 Einheiten auf den Markt kommen.
Ermitteln Sie die Marktabgaben von R und S sowie den Koeffizienten a33 ,
und erläutern Sie kurz dessen Bedeutung.
Aufgabe 9
(aus Abi 2000)
Drei Firmen A, B und C sind nach dem Leontiefmodell miteinander verflochten.
Die gegenseitig und für den Markt erbrachten Leistungen werden in Verrechnungseinheiten
in folgender Tabelle zusammengestellt :
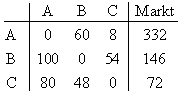 1. Stellen Sie die Inputmatrix auf und erläutern Sie, welche Bedeutung es für den
Produktionsprozess hat, dass in der Inputmatrix eine Diagonale nur Nullen enthält.
1. Stellen Sie die Inputmatrix auf und erläutern Sie, welche Bedeutung es für den
Produktionsprozess hat, dass in der Inputmatrix eine Diagonale nur Nullen enthält.
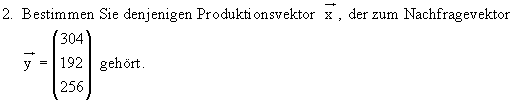
Aufgabe 10
(aus Abi 2001)
Die drei Abteilungen F, G und H eines Unternehmens sind nach dem Leontief-Modell
miteinander verbunden ( Angaben in Mengeneinheiten ME ) :
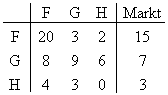 1. Bestimmen Sie die Inputmatrix A .
2. Es wird eine Produktionserhöhung in Abteilung F um 20 und in Abteilung G um 30 Einheiten
bei gleichbleibender Produktion in H vorgeschlagen.
Beurteilen Sie anhand des neuen Marktvektors, ob dies möglich ist.
1. Bestimmen Sie die Inputmatrix A .
2. Es wird eine Produktionserhöhung in Abteilung F um 20 und in Abteilung G um 30 Einheiten
bei gleichbleibender Produktion in H vorgeschlagen.
Beurteilen Sie anhand des neuen Marktvektors, ob dies möglich ist.
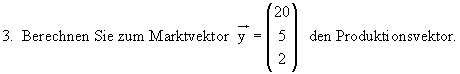 4. Nun soll Abteilung F die Produktion auf 60 ME erhöhen und die Abteilungen F und G sollen
jeweils mindestens 20 ME an den Markt abgeben. Stellen Sie die drei sich ergebenden Bedingungen
4. Nun soll Abteilung F die Produktion auf 60 ME erhöhen und die Abteilungen F und G sollen
jeweils mindestens 20 ME an den Markt abgeben. Stellen Sie die drei sich ergebenden Bedingungen
 den Bereich für die zugehörigen Produktionszahlen in den Abteilungen G und H .
den Bereich für die zugehörigen Produktionszahlen in den Abteilungen G und H .
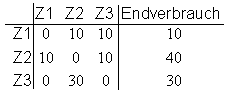 a) Berechnen Sie die Inputmatrix nach dem Leontief-Modell.
b) Wieviele Mengeneinheiten stehen für den Endverbrauch zur Verfügung,
wenn im 1. Zweigwerk 100 ME, im 2. Zweigwerk 180 ME und
im 3. Zweigwerk 120 ME produziert werden?
c) In der nächsten Produktionsperiode benötigt man für den Endverbrauch 60 ME vom
Werk Z1, 75 ME vom Werk Z2 und 90 ME vom Werk Z3.
Berechnen Sie, wieviele ME dann in den einzelnen Zweigwerken produziert werden müssen.
a) Berechnen Sie die Inputmatrix nach dem Leontief-Modell.
b) Wieviele Mengeneinheiten stehen für den Endverbrauch zur Verfügung,
wenn im 1. Zweigwerk 100 ME, im 2. Zweigwerk 180 ME und
im 3. Zweigwerk 120 ME produziert werden?
c) In der nächsten Produktionsperiode benötigt man für den Endverbrauch 60 ME vom
Werk Z1, 75 ME vom Werk Z2 und 90 ME vom Werk Z3.
Berechnen Sie, wieviele ME dann in den einzelnen Zweigwerken produziert werden müssen.
 a) Berechnen Sie die Werte von a, b und c und stellen Sie die gegenseitige Verfechtung der
Sektoren in einer Tabelle dar.
b) Welcher Konsumvektor ergibt sich bei einem Produktionsvektor ( 40 50 30 )T ?
c) Wieviele Einheiten müssen die Sektoren in einer Periode produzieren, wenn der
Konsumvektor ( 18 24 12 )T beträgt ?
a) Berechnen Sie die Werte von a, b und c und stellen Sie die gegenseitige Verfechtung der
Sektoren in einer Tabelle dar.
b) Welcher Konsumvektor ergibt sich bei einem Produktionsvektor ( 40 50 30 )T ?
c) Wieviele Einheiten müssen die Sektoren in einer Periode produzieren, wenn der
Konsumvektor ( 18 24 12 )T beträgt ?
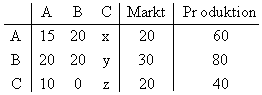 a) Berechnen Sie, welche Mengeneinheiten an den Sektor C geliefert wurden und bestimmen
Sie die Inputmatrix, die zu dieser Verflechtung gehört.
b) Die Nachfrage nach den Produkten der Sektoren A und B steigt, während die Nachfrage nach den
Produkten des Sektors C unverändert bleibt. Man beschließt daher, die Produktion des
Sektors A um 20 % und die Produktion von B um 40 % zu steigern.
Wieviele Mengeneinheiten mehr müssen dann im Sektor C produziert werden?
c) Für die nächste Produktionsperiode rechnet man mit einer geänderten Nachfrage.
Man geht davon aus, dass von den Produkten des Sektors A 24 Einheiten,
von Sektor B 20 Einheiten und von C 16 Einheiten nachgefragt werden.
Wieviel wird dann in den einzelnen Sektoren produziert werden, wenn man sich an diese neue
Situation anpasst?
a) Berechnen Sie, welche Mengeneinheiten an den Sektor C geliefert wurden und bestimmen
Sie die Inputmatrix, die zu dieser Verflechtung gehört.
b) Die Nachfrage nach den Produkten der Sektoren A und B steigt, während die Nachfrage nach den
Produkten des Sektors C unverändert bleibt. Man beschließt daher, die Produktion des
Sektors A um 20 % und die Produktion von B um 40 % zu steigern.
Wieviele Mengeneinheiten mehr müssen dann im Sektor C produziert werden?
c) Für die nächste Produktionsperiode rechnet man mit einer geänderten Nachfrage.
Man geht davon aus, dass von den Produkten des Sektors A 24 Einheiten,
von Sektor B 20 Einheiten und von C 16 Einheiten nachgefragt werden.
Wieviel wird dann in den einzelnen Sektoren produziert werden, wenn man sich an diese neue
Situation anpasst?
 a) Bestimmen Sie die Inputmatrix.
a) Bestimmen Sie die Inputmatrix.
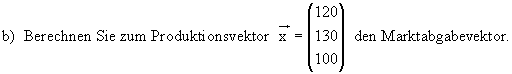
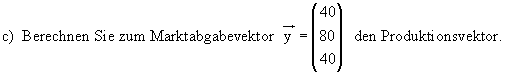 d) Für den kommenden Produktionszeitraum erwartet man, dass sich die Nachfrage nach
den Gütern von B und C nicht ändert, aber die Nacgfrage nach den Gütern von A steigt.
Man beschließt daher, die Produktion im Sektor A um 70 ME zu erhöhen.
( Die Angaben beziehen sich auf die anfangs gegebene Tabelle, nicht auf die Aufgabe b und c.)
Um wieviele ME steigt dann auch die Produktion in den Sektoren B und C ?
d) Für den kommenden Produktionszeitraum erwartet man, dass sich die Nachfrage nach
den Gütern von B und C nicht ändert, aber die Nacgfrage nach den Gütern von A steigt.
Man beschließt daher, die Produktion im Sektor A um 70 ME zu erhöhen.
( Die Angaben beziehen sich auf die anfangs gegebene Tabelle, nicht auf die Aufgabe b und c.)
Um wieviele ME steigt dann auch die Produktion in den Sektoren B und C ?
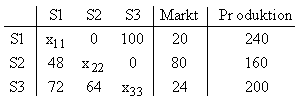 a) Bestimmen Sie die Inputmatrix, die zu dieser Verflechtung gehört.
b) Wie groß muss die Produktion in jedem der Sektoren sein, wenn eine Marktabgabe
a) Bestimmen Sie die Inputmatrix, die zu dieser Verflechtung gehört.
b) Wie groß muss die Produktion in jedem der Sektoren sein, wenn eine Marktabgabe
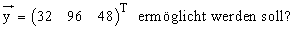
 d) Für die nächste Periode plant man in S1 eine Produktion von 300 ME,
in S2 von 220 ME. Jeder Sektor soll so viel produzieren, dass von den Gütern jedes
Sektors mindestens 20 ME an den Markt abgegeben werden können.
Wieviele ME muss man dann in S3 mindestens, höchstens produzieren?
e) Im folgenden hängt der Produktionsvektor von einer positiven Variablen a ab.
d) Für die nächste Periode plant man in S1 eine Produktion von 300 ME,
in S2 von 220 ME. Jeder Sektor soll so viel produzieren, dass von den Gütern jedes
Sektors mindestens 20 ME an den Markt abgegeben werden können.
Wieviele ME muss man dann in S3 mindestens, höchstens produzieren?
e) Im folgenden hängt der Produktionsvektor von einer positiven Variablen a ab.
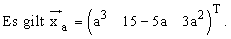 Beim Verkauf erzielt man bei den Gütern von S1 und S3 jeweils 15 GE ( Geldeinheiten ),
bei S2 30 GE pro Mengeneinheit.
Bei welchem Wert von a nehmen die Gesamteinnahmen ein relatives Maximum an ?
Beim Verkauf erzielt man bei den Gütern von S1 und S3 jeweils 15 GE ( Geldeinheiten ),
bei S2 30 GE pro Mengeneinheit.
Bei welchem Wert von a nehmen die Gesamteinnahmen ein relatives Maximum an ?

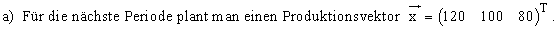 Wieviele Mengeneinheiten werden dann von den Zweigwerken an den Markt abgegeben?
b) Berechnen Sie den Marktabgabe- und den Produktionsvektor für den Fall, dass alle
Zweigwerke gleich viel an den Markt abgeben und im 3. Zweigwerk 66 Menheneinheiten
produziert werden.
Wieviele Mengeneinheiten werden dann von den Zweigwerken an den Markt abgegeben?
b) Berechnen Sie den Marktabgabe- und den Produktionsvektor für den Fall, dass alle
Zweigwerke gleich viel an den Markt abgeben und im 3. Zweigwerk 66 Menheneinheiten
produziert werden.
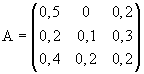 a) In der vergangenen Produktionsperiode stellte Sektor A insgesamt 400 Mengeneinheiten ( ME ) her,
Sektor B 600 ME und Sektor C 500 ME. Geben Sie in einer Tabelle an, wieviele Mengeneinheiten
die Sektoren untereinander austauschten und an den Konsum abgaben.
b) In der laufenden Produktionsperiode rechnet man mit einer Nachfrage von 125 ME nach den
Gütern von A, 300 ME nach den Gütern von B und 150 ME nach den Gütern von C.
Bestimmen Sie die entsprechenden Produktionsmengen in den einzelnen Sektoren.
a) In der vergangenen Produktionsperiode stellte Sektor A insgesamt 400 Mengeneinheiten ( ME ) her,
Sektor B 600 ME und Sektor C 500 ME. Geben Sie in einer Tabelle an, wieviele Mengeneinheiten
die Sektoren untereinander austauschten und an den Konsum abgaben.
b) In der laufenden Produktionsperiode rechnet man mit einer Nachfrage von 125 ME nach den
Gütern von A, 300 ME nach den Gütern von B und 150 ME nach den Gütern von C.
Bestimmen Sie die entsprechenden Produktionsmengen in den einzelnen Sektoren.
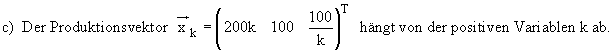 Für welche Werte von k (auf 2 Dezimalen) ist die Marktabgabe von B größer als
die Marktabgabe von Sektor A ?
d) Für die nächste Produktionsperiode hat man vor, die Fertigung umzustellen.
Dadurch ändern sich die Koeffizienten a13 und a23 der Inputmatrix.
Die Gesamtproduktionen der Sektoren A, B und C verhalten sich dann wie 5:3:4 .
Berechnen Sie die neue Inputmatrix und den neuen Produktionsvektor für einen
Für welche Werte von k (auf 2 Dezimalen) ist die Marktabgabe von B größer als
die Marktabgabe von Sektor A ?
d) Für die nächste Produktionsperiode hat man vor, die Fertigung umzustellen.
Dadurch ändern sich die Koeffizienten a13 und a23 der Inputmatrix.
Die Gesamtproduktionen der Sektoren A, B und C verhalten sich dann wie 5:3:4 .
Berechnen Sie die neue Inputmatrix und den neuen Produktionsvektor für einen
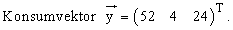
 1. Erstellen Sie die zugehörige Input-Output-Tabelle, die auch den Konsumvektor erhält.
2. Die Produktion des Sektors R soll um a Einheiten erniedrigt werden, während die
Produktionseinheiten bei S und T konstant bleiben sollen.
Bestimmen Sie den maximal möglichen Wert von a .
3. Durch eine Umorganisation in Sektor T wurde erreicht, dass sich der Koeffizient a33 verändert.
Dadurch ergibt sich für den Produktionsvektor aus obiger Angabe,
dass von Sektor T 7 Einheiten auf den Markt kommen.
Ermitteln Sie die Marktabgaben von R und S sowie den Koeffizienten a33 ,
und erläutern Sie kurz dessen Bedeutung.
1. Erstellen Sie die zugehörige Input-Output-Tabelle, die auch den Konsumvektor erhält.
2. Die Produktion des Sektors R soll um a Einheiten erniedrigt werden, während die
Produktionseinheiten bei S und T konstant bleiben sollen.
Bestimmen Sie den maximal möglichen Wert von a .
3. Durch eine Umorganisation in Sektor T wurde erreicht, dass sich der Koeffizient a33 verändert.
Dadurch ergibt sich für den Produktionsvektor aus obiger Angabe,
dass von Sektor T 7 Einheiten auf den Markt kommen.
Ermitteln Sie die Marktabgaben von R und S sowie den Koeffizienten a33 ,
und erläutern Sie kurz dessen Bedeutung.
 1. Stellen Sie die Inputmatrix auf und erläutern Sie, welche Bedeutung es für den
Produktionsprozess hat, dass in der Inputmatrix eine Diagonale nur Nullen enthält.
1. Stellen Sie die Inputmatrix auf und erläutern Sie, welche Bedeutung es für den
Produktionsprozess hat, dass in der Inputmatrix eine Diagonale nur Nullen enthält.
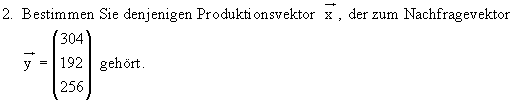
 1. Bestimmen Sie die Inputmatrix A .
2. Es wird eine Produktionserhöhung in Abteilung F um 20 und in Abteilung G um 30 Einheiten
bei gleichbleibender Produktion in H vorgeschlagen.
Beurteilen Sie anhand des neuen Marktvektors, ob dies möglich ist.
1. Bestimmen Sie die Inputmatrix A .
2. Es wird eine Produktionserhöhung in Abteilung F um 20 und in Abteilung G um 30 Einheiten
bei gleichbleibender Produktion in H vorgeschlagen.
Beurteilen Sie anhand des neuen Marktvektors, ob dies möglich ist.
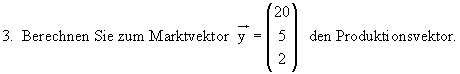 4. Nun soll Abteilung F die Produktion auf 60 ME erhöhen und die Abteilungen F und G sollen
jeweils mindestens 20 ME an den Markt abgeben. Stellen Sie die drei sich ergebenden Bedingungen
4. Nun soll Abteilung F die Produktion auf 60 ME erhöhen und die Abteilungen F und G sollen
jeweils mindestens 20 ME an den Markt abgeben. Stellen Sie die drei sich ergebenden Bedingungen
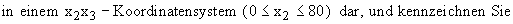 den Bereich für die zugehörigen Produktionszahlen in den Abteilungen G und H .
den Bereich für die zugehörigen Produktionszahlen in den Abteilungen G und H .
