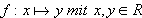gemäß der Zuordnungsvorschrift 
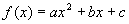.Seminararbeit von Melanie Wagner, 13e
Nachbearbeitung und Ergänzung: OStR Starfinger
Eine quadratische Funktion ist eine Abbildung 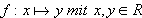gemäß der Zuordnungsvorschrift .
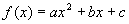Die Nullstellen der quadratischen Funktion bekommt man durch Lösen der zugehörigen quadratischen Gleichung.
Formen der Gleichung einer quadratischen Funktion sind:
Normalform: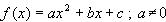 
Produktform: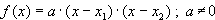 
Scheitelform: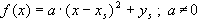 
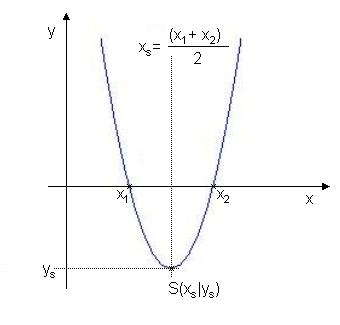
Der Graph der quadratischen Funktion ist definiert als die Punktmenge in der x,y- Ebene,
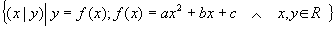
Der Graph 
einer quadratischen Funktion f heißt Parabel.
Ihr höchster oder tiefster Punkt heißt Scheitelpunkt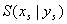 
.
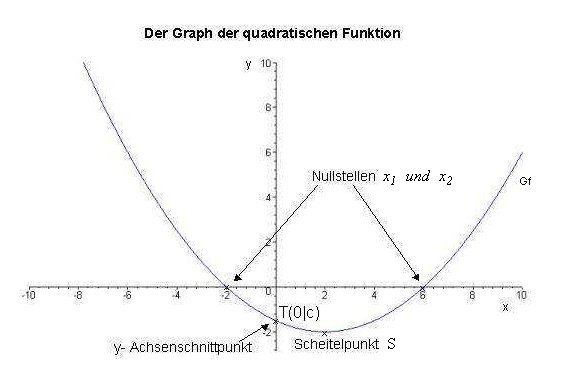
Bild 1: Normalparabel
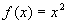; (hier ist a=1, b=0 und c=0)
Hier gilt: f(x) = (x – 0)2 + 0, d. h. der Scheitel hat die Koordinaten (0 | 0).
Bild 2: Verschiebung in y-Richtung
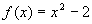; ( hier ist a=1, b=0, c=-2)
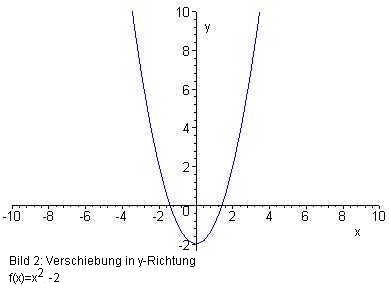
Hier gilt: f(x) = (x – 0)2 – 2, d. h. der Scheitel hat die Koordinaten (0 | –2).
Bild 3: Verschiebung in x-Richtung
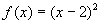
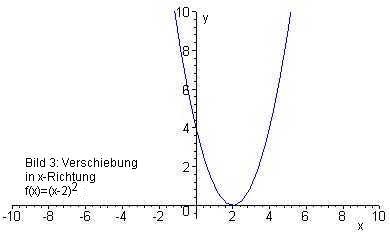
Hier gilt: f(x) = (x – 2)2 + 0, d. h. der Scheitel hat die Koordinaten (2 | 0).
Bild 4: Verschiebung in x- und y- Richtung
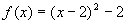
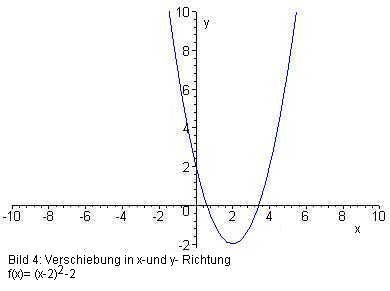
Hier hat der Scheitel die Koordinaten (2 | –2).
Bild 5: Normalparabel nach unten geöffnet
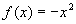; (a < 0)
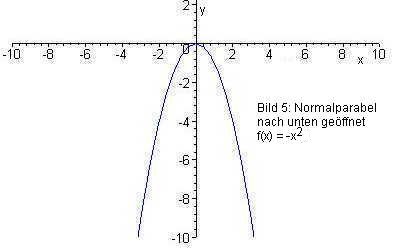
Hier gilt: f(x) = – (x – 0)2 + 0, d. h. der Scheitel hat die Koordinaten (0 | 0).
Bild 6: Streckung der Parabel in Richtung y- Achse um den Faktor 2
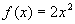; (a > 1)
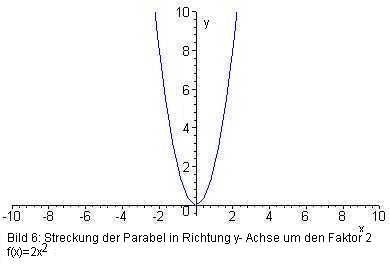
Hier gilt: f(x) = 2(x – 0)2 + 0, d. h. der Scheitel hat die Koordinaten (0 | 0).
Bild 7: Streckung der Parabel in Richtung y- Achse um den Faktor 0,5
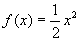; (also a < 1)
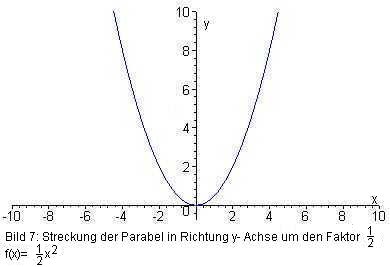
Um den Graphen zu zeichnen, ist es vorteilhaft, einige seiner wichtigen Eigenschaften zu kennen, wie:
• den Scheitelpunkt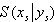 
des Graphen
• die Nullstellen der Funktion (x- Koordinate der Schnittpunkte mit der x- Achse)
• y- Achsenabschnitt des Graphen ( also : f(0) )
Es kann auch eine Wertetabelle als Zeichenhilfe angelegt werden.
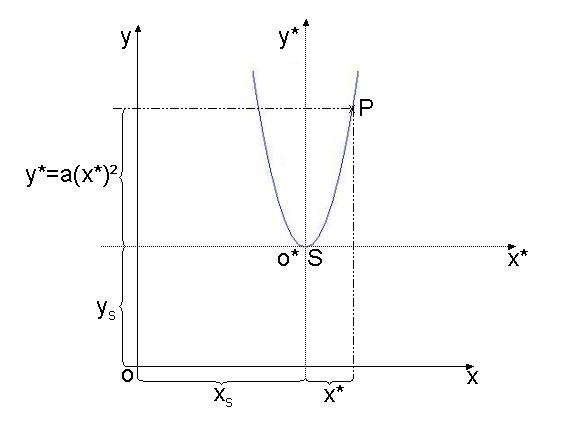
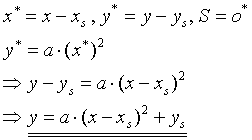
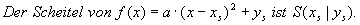
Sonderfälle von Parabelgleichungen in Scheitelform sind:
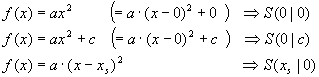
Die Scheitelform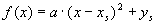 
kann durch Ausmultiplizieren
in die Normalform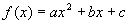 
verwandelt werden.
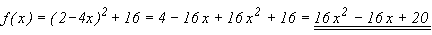
Wenn die Scheitelform 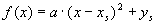gegeben ist, kann man sie
ausmultiplizieren: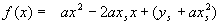 
Durch Koeffizientenvergleich mit der Normalform 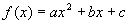ergeben sich dann die beiden Gleichungen :
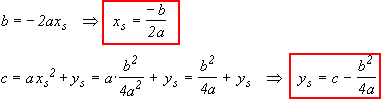
Damit lassen sich die Scheitelkoordinaten aus der Normalform bestimmen.
Hinweis: Für ys braucht man nicht unbedingt die angegebene Formel, sondern wegen ys = f (xs ) kann man ys auch einfach durch Einsetzen von xs in die Normalform bestimmen.
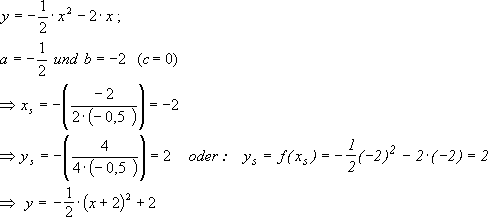
Eine quadratische Gleichung hat die Form: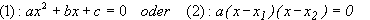 
Zu (2): Die Lösungen der Produktform sind: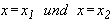 
.
Zu (1): Sie kann maximal zwei Lösungen haben.
Um die Lösungsformel zu bestimmen, setzt man die Formeln für die Scheitelkoordinaten in die Scheitelform ein, setzt diese gleich Null und löst dann nach x auf:
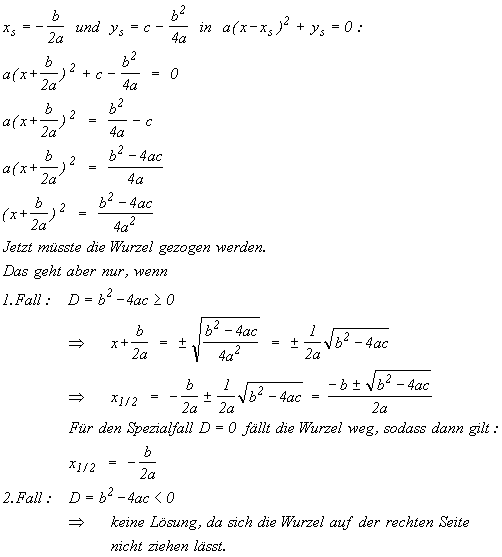
Man bezeichnet den unter dem Wurzelzeichen vorkommenden Ausdruck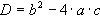 
als
die Diskriminante („Unterscheidende“) der quadratischen Gleichung, da dieser Term zwischen
den verschiedenen Lösungseigenschaften der quadratischen Gleichung unterscheidet.
Die x- Koordinaten der Schnittpunkte der Graphen einer quadratischen Funktion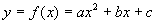 
mit der x- Achse (y=0), nennt man auch die Nullstellen der Funktion f(x).
Die damit geltenden Gleichungen
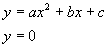
ergeben die quadratische Gleichung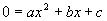 
, deren Lösungen die Nullstellen sind.
Zusammenfassend gilt: Wenn
D = 0, dann liegt eine doppelte Nullstelle vor: (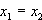 
)
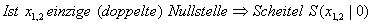
D > 0, dann liegen zwei einfache Nullstellen vor: (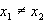
)
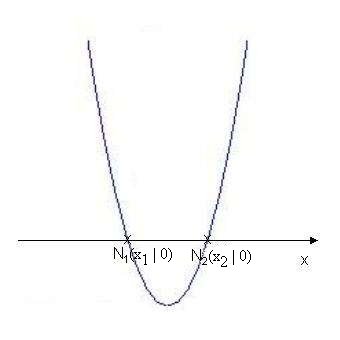
D < 0, dann liegt keine Nullstelle vor, d. h. die Parabel schneidet die x-Achse nicht!
Wenn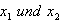 
zwei verschiedene Nullstellen sind, bekommt man 
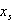auch durch die Formel
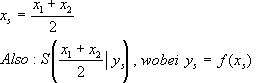
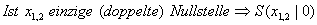
Übungsbeispiele zu quadratischen Gleichungen
Übungsbeispiele zur Scheitel- und Nullstellenbestimmung
Übungsbeispiele zum Schnitt von Parabeln mit Geraden oder Parabeln
Sind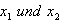 
zwei Nullstellen 
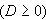der Funktion 
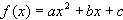, so lässt sich diese Funktion
in Linearfaktoren zerlegen, nämlich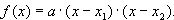 
Begründung: Beide Funktionsterme repräsentieren zwei Parabeln mit demselben Öffnungsfaktor a
und denselben Nullstellen. Da es jedoch nur eine Parabel mit diesen Eigenschaften gibt,
müssen die beiden Funktionsterme identisch sein.
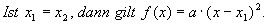
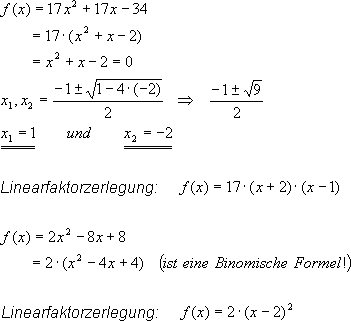
Rechnet man man für a = 1 die Produktdarstellung von f aus, so ergibt sich:
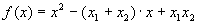
Daraus ergibt sich für a = 1 der Satz von Vieta:
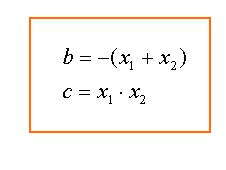
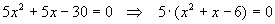
Die Nullstellen von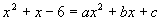 
ergeben sich durch Raten nach dem Satz von Vieta.
Danach gilt:
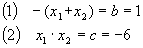
1.Vermutung: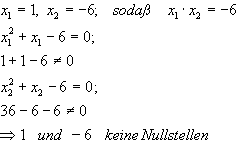 
2. Vermutung: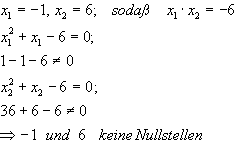 
3. Vermutung: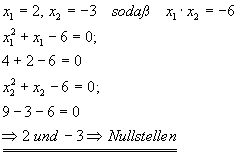 
Ungleichungen können wie Gleichungen gelöst werden, man muss aber das Ungleichheitszeichen beibehalten.
Allgemein gilt, dass für eine Ungleichung stets eines der Zeichen <,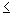 
, >, 
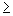verwendet wird.
Bei Ungleichungen müssen zwei Besonderheiten beachtet werden!
(1): Wird eine Ungleichung mit einer negativen Zahl multipliziert oder durch eine negative Zahl dividiert,
so muss das >,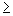 
, <, 
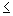- Zeichen umgedreht werden.
(2): In Ungleichungen führen oft unendlich viele verschiedene x-Werte zu einer wahren Aussage.
Die Lösungsmenge einer Ungleichung kann also ein Wertebereich sein,
der unendlich viele Werte enthält.
Schreibweisen von Lösungsmengen:
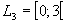bedeutet, dass die Werte 0 bis 2,999999… in der Lösungsmenge enthalten
sind. Der Wert 3 gehört jedoch nicht mehr dazu. Darstellung einer Lösungsmenge
mit eckigen Klammern wird Intervalldarstellung genannt!
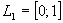ist ein geschlossenes Intervall: die Grenzen 0 bzw. 1 gehören zum Intervall.
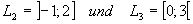sind halboffene Intervalle, da die untere Grenze bei 
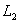bzw.
die obere Grenze bei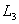 
nicht innerhalb des Intervalls liegen.
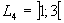ist ein offenes Intervall, da beide Grenzen nicht enthalten sind.
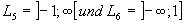sind offene 
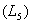bzw. halboffene 
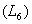Intervalle. Das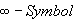 
bedeutet Unendlich, d.h.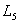 
hat nach oben keine Grenze, 
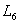ist nach unten unbeschränkt.
Für die Lösungsmenge von Ungleichungen gibt es drei Möglichkeiten:
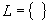
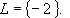
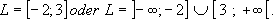
(1)
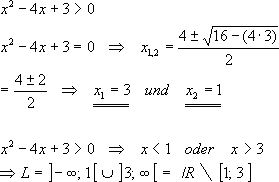
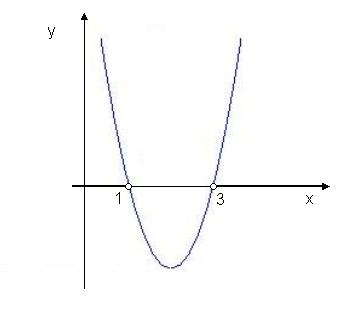
(2)
Eine Schar von quadratischen Funktionen ist eine Menge solcher Funktionen mit demselben
Funktionsterm, der außer von der unabhängigen Variablen x auch noch von einem variablen
Parameter a, b, c, t, k, usw. abhängt.
Die Schar der zugehörigen Graphen bezeichnet man auch als Parabelschar.
Viele ihrer Eigenschaften sind vom Scharparameter abhängig. Um sie zu diskutieren, ist es oft
notwendig, Fallunterscheidungen zu treffen. Es kann vorkommen, dass im beschreibenden
Term der zu untersuchenden Eigenschaft der Scharparameter in einem Nenner oder in einem
Radikanden des Terms auftritt. Dann muss gelten
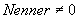und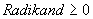 
.
Aufgabe:
1. Gegeben sei die quadratische Kurvenschar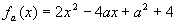 
a) Welche Scharkurve geht durch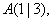 
?
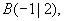
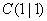b) Welche Punkte der y-Achse sind Parabelpunkte ?
c) Bestimme die Nullstellen und ihre Vielfachheit.
d) Untersuche, ob es Paare von Scharkurven gibt, die symmetrisch bezüglich des Koordinatensystems liegen.
e) Bestimme die Scheitel der Schar und die Kurve, auf der sie liegen
.
Lösung:
1.a)
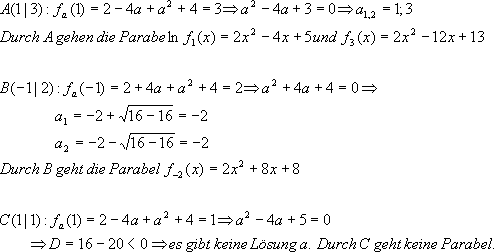
b) Die Menge der Parabelpunkte auf der y- Achse ist gegeben durch:
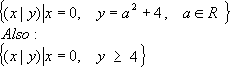
c)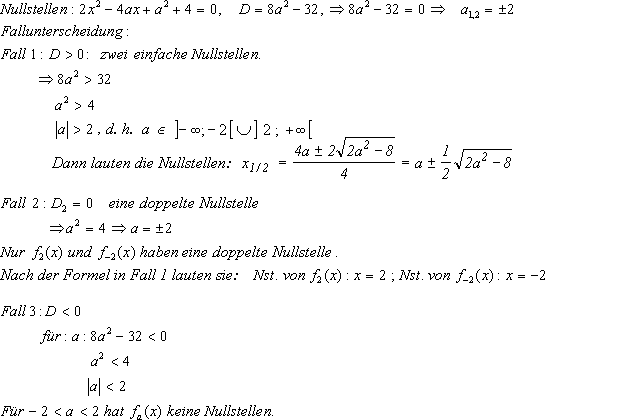 
d) Symmetrie im Koordinatensystem
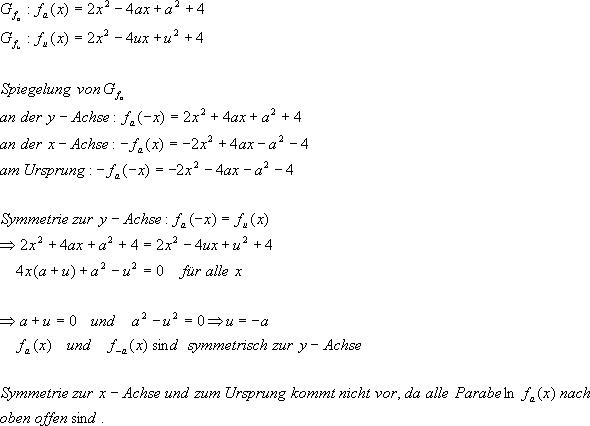
e) Scheitel der Parabelschar:
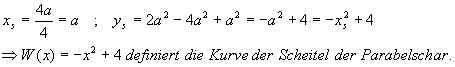
Quadratische Funktionen kommen vielfach in der Physik und den Ingenieurwissenschaften zur Anwendung.
In der Mathematik wird als Variable normalerweise immer x verwendet. In der Physik dagegen werden
Variablen mit unterschiedlichen Buchstaben bezeichnet, je nachdem für welche physikalische Größe die
Variable eingesetzt wird. Für die Berechnung ändert sich dadurch nichts.
Du stehst auf dem Olympiaturm und möchtest durch ein Panoramafernglas die herrliche Aussicht genießen.
Dazu benötigst Du eine Münze. Nun fällt Dir die Münze leider hinunter.
Wie Du weißt, macht es keinen Sinn den Turm hinunter zu laufen und die Münze aufzufangen.
Wie lange dauert es, bis die Münze am Boden ankommt?
Der physikalische Zusammenhang zwischen der Fallhöhe s und der Fallzeit t lautet:
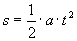
s = Fallhöhe
a = Fallbeschleunigung
t = Zeit (time)
Die Fallbeschleunigung beträgt auf der Erde ca.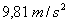 
(auf dem Mond wäre es nur 
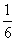davon).
Der Münchener Olympiaturm ist ca. 290 m hoch.
Nun lautet die Gleichung:
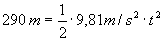
Nun überlegt man sich die passende Definitionsmenge. Es hat sicher keinen Sinn, negative Werte für die Zeit zuzulassen.
Auch die 0 wird nicht zugelassen, da die Fallzeit > 0 Sekunden ist.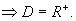 
Da die Fallzeit bestimmt werden soll, wird die Gleichung nach t aufgelöst.
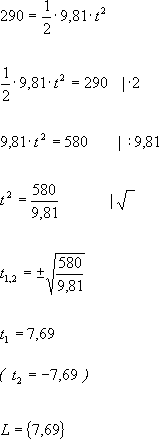
Es dauert also 7,69 Sekunden, bis die Münze am Boden ankommt. Der Luftwiderstand wurde nicht berücksichtigt,
weil er auf den freien Fall einer Geldmünze einen vernachlässigbar kleinen Einfluss hat.
Anders wäre es z.B. bei einer Eintrittskarte, hier spielt der Luftwiderstand eine große Rolle.
