
Einführung in ‚JavaSketchPad‘
Version 4
Peter Starfinger, 2004, BOS Sozialwesen München
Inhaltsverzeichnis
Vorstellung und Einrichtung von JavaSketchPad
JavaSketchPad (JSP) ist die kostenlose Internet-Version des interaktiven Geometrieprogramms „The Geometer's Sketchpad“. Ohne sich umständlich in Java einarbeiten zu müssen, kann man mit JSP selbstständig ein Geometrie- oder Analysisapplet erstellen und in eine eigene HTML-Datei einbinden. Dazu muss das Applet innerhalb der HTML-Datei mit Hilfe von Applet-Parametern definiert werden, die auch die gewünschten Konstruktionsangaben enthalten. Zur Erstellung der Konstruktion muss man sich allerdings die JSP-Konstruktionssprache aneignen. Auf den ersten Blick scheint dies im Vergleich zu Geometrieprogrammen wie z. B. GEONExT von der Universität Bayreuth oder Z.u.L. von der Kath. Universität Eichstätt, die nahezu keine Syntaxkenntnisse erfordern und geometrische Konstruktionen alleine mit der Maus ermöglichen, einen Nachteil darzustellen. Andererseits sind nachträgliche Korrekturen an früheren Konstruktionsschritten in solchen Programmen schwierig oder gar unmöglich, stellen aber in einem syntaxorientierten Geometrieprogramm wie JavaSketchPad keinerlei Problem dar. Außerdem ist es vorteilhaft, dass JSP vergleichsweise schnell, stabil und ohne große Systemanforderungen auf jedem Browser läuft. Ein ausführlicher Vergleich von JavaSketchPad mit den beiden Applikationen GEONExT und Z.u.L. mit anschließender Gesamtbewertung findet sich hier.
Die Arbeit mit JSP erfordert das Java-Archiv ‚jsp4.jar‘, das hier heruntergeladen werden kann (ursprüngliche Quelle: www.keypress.com). (Eine selbst startende CD-ROM, die neben der notwendigen JavaSketchPad-Software die vorliegende Einführung und den JSP-Generator enthält, kann als Image (ISO-Datei) hier heruntergeladen werden.)
Im Gegensatz zu GEONExT oder Z.u.L. gibt es hier also keine eigene Entwicklungsoberfläche für die geplante geometrische Konstruktion. Daher ist es entweder ratsam, einen HTML-Editor und einen Webbrowser nebeneinander geöffnet zu haben und mit dem Webbrowser die Zwischenstufen der JSP-Konstruktion immer wieder zu kontrollieren. Eine zweite Möglichkeit der Erstellung einer JSP-Konstruktion, nämlich mit Hilfe eines JSP-Code-Generators, wurde von dem Niederländer Hans Klein geschaffen und von mir zu einer praktikablen browsergestützten Arbeitsoberfläche ausgebaut. Dieser JSP-Generator erweitert die Möglichkeiten von JavaSketchPad, indem er den Umgang mit Variablen sowie eine modulare Struktur gestattet, was den Aufbau regelrechter Bibliotheken mit aufrufbaren geometrischen Grundkonstruktionen ermöglicht. Der Generator wird weiter unten ausführlich vorgestellt. Am Ende dieser Einführung schließt sich noch eine JSP-Modul-Bibliothek an, die fortlaufend erweitert wird.
Beispiel eines HTML-Arbeitsblattes mit JavaSketchPad
Im Folgenden wird der kommentierte Quellcode eines HTML-Arbeitsblattes mit einer JavaSketchPad-Konstruktion zusammen mit dem Arbeitsblatt selbst in zwei nebeneinanderstehenden Frames vorgestellt. Anhand dieses Arbeitsblattes soll der Schüler / die Schülerin die Eigenschaften eines (dynamischen) Koordinatensystems kennen lernen. Sie werden genau sehen, wie der Browser die einzelnen HTML-Tags (= HTML-Anweisungen) interpretiert. Wenn Sie im Quellcode den Mauszeiger auf einen Tag stellen, erscheint zu diesem Tag eine kurze Erklärung. Öffnen Sie bitte nun diese HTML-Datei, machen Sie sich mit ihr vertraut und schließen Sie sie anschließend wieder.
Sie sehen, dass die Formatierung des Quellcodes (Zeilenumbrüche, Tabs, mehrere (nicht erzwungene) Leerzeichen hintereinander, die in den Einstellungen des Editors gewählte Art und Größe der Schrift usw.) in der Browser-Darstellung des Textes nicht erscheint. Anders ausgedrückt: Sie müssen Ihre gewünschten Textformatierungen mit Hilfe von HTML-Tags angeben und diese an der richtigen Stelle wieder schließen.
Es gibt allerdings einen HTML-Tag, der die Identität von Quellcodeformatierung und Textformatierung erzwingt, nämlich „<PRE>“. Dieser Tag leitet einen „vorformatierten“ Text ein, an dessen Ende „</PRE>“ stehen muss. Ohne spezielle HTML-Kenntnisse lassen sich mit diesem Tag Arbeitsblätter bequem erstellen. Allerdings schaltet <PRE> auf die wenig ansprechende Schriftart „Courier“ um. Dies können Sie vermeiden, indem Sie nach dem <PRE>-Tag noch den Tag <FONT FACE="(gewünschte Schriftart,
Mit dem <PRE>-Tag hat der Textteil des Beispiel-Quellcodes die folgende einfachere Gestalt:
. . .
<PRE><FONT FACE="Times New Roman" SIZE="3">
<B>Arbeitsauftrag:</B>
1. Verschiebe den Koordinatenursprung.
2. Verschiebe den Einheitspunkt auf der x-Achse.
3. Verschiebe den Punkt P und beobachte seine links oben eingeblendeten Koordinaten.
4. Die Achsen teilen das Koordinatensystem in vier Quadranten.
Beantworte mit Hilfe des Punktes P die folgenden Fragen:<sub> </sub>
o Wo liegt der 1. Quadrant, der nur Punkte mit positiven Koordinaten enthält?
o Wo liegt der 2. Quadrant, in dem die x-Koordinaten negativ und die y-Koordinaten
positiv sind?
o Wo liegt der 3. Quadrant, in dem beide Koordinaten negativ sind?
o Wo liegt der 4. Quadrant, in dem die x-Koordinaten positiv und die y-Koordinaten
negativ sind?
5. Drücke die Taste ' r '.
Quelle von JavaSketchpad: <A href="http://www.keypress.com/">http://www.keypress.com/</A>
</FONT></PRE>
. . .
Öffnen Sie zum Vergleich auch diese HTML-Datei mit Ihrem Browser. Sie sehen, dass deren Erscheinungsbild sich von dem der HTML-Datei ohne <PRE>-Tag kaum unterscheidet. Einschränkend muss allerdings betont werden, dass Sie bei Verwendung des <PRE>-Tags für Ihren Text von vornherein nur die (bescheidenen) Formatierungsangebote Ihres Editors nutzen und damit die ungleich vielfältigeren und einem Textverarbeitungsprogramm wie Word ebenbürtigen Formatierungsmöglichkeiten, die HTML bietet, ungenutzt lassen.
Um sich in die Welt der HTML-Tags einzuarbeiten, empfehle ich die ausgezeichnete Webseite SELFHTML von Stefan Münz, meinem sehr geschätzten HTML-Lehrer. Ich persönlich bin davon überzeugt, dass sich dieser Aufwand rentiert.
Zwar nimmt die Ansicht zu, dass sich angesichts so komfortabler Webseiten-Kreatoren wie des (kostenpflichtigen) „DreamWeaver“ ein eigenständiges Aneignen von HTML nicht mehr lohne. Den Verfechtern dieser Meinung wünsche ich nur, dass sie ihre superbequemen HTML-Utilities immer in ihrer Nähe haben. Außerdem zeigt die Erfahrung, dass auch das komfortabelste Webseiten-Erstellungsprogramm oftmals eine manuelle Nachbearbeitung des Quellcodes erfordert, was ohne eigene HTML-Kenntnisse schwierig ist.
Der JavaSketchPad-Generator
1. Arbeitsweise des JSP-Generators
In JavaSketchPad stellt man den Bezug zu einem vorangegangenen Konstruktionsschritt über dessen Zeilennummer her. Wenn man dann nachträglich einen Schritt einfügen will, stimmen die nachfolgenden Zeilenbezüge nicht mehr und müssen aufwändig korrigiert werden. Im von mir überarbeiteten und ergänzten JavaSketchPad-Generator von dem Niederländer Hans Klein ist dieser Nachteil beseitigt, denn hier besteht die Möglichkeit, die einzelnen Konstruktionsschritte mit Variablen zu bezeichnen, auf die dann später zurückgegriffen werden kann. Ein Beispiel soll dies verdeutlichen.
| In JavaSketchPad kann man leider nur Punkte und keine anderen geometrischen Objekte beschriften. Im Folgenden sollen aber beispielsweise die Seiten eines Dreiecks beschriftet werden. Dazu muss man, vereinfacht dargestellt, zunächst den jeweiligen Seitenmittelpunkt konstruieren (Zeilen 7, 18, 26) und diesen dann beschriften. Tatsächlich empfiehlt es sich aber, noch einen mittelpunktsnahen unsichtbaren Hilfspunkt zu konstruieren (Zeilen 8-15, 19-23, 27-31) und diesen dann zu beschriften, weil sonst die Beschriftung zu eng an der Seite positioniert wäre, was optisch irritiert. Für die Beschriftung selbst ist das von JavaSketchPad standardmäßig für Punkte angebotene „label“ insofern unbefriedigend, als es innerhalb des Applets bezüglich der gewählten Schriftart, der Zeichengröße sowie der Schriftfarbe nicht gestaltungsfähig, sondern völlig statisch ist. Abhilfe ist nur möglich, indem man statt des üblichen Punkt-Labels zunächst einen Text definiert (Zeilen 16, 24, 32) und diesen dann mit der gewünschten Formatierung an den Hilfspunkt heftet (Zeilen 17, 25, 33). Nun zum Konstruktionstext mit dem zugehörigen Applet: | ||
|
{1} Point(170,300); |
|
|
| In der JSP-Generator-Syntax lautet dieser Text z. B. wie folgt: | ||
|
A=Point(170,300,'') |
||
|
Im vorstehenden Konstruktionstext wird dreimal, nämlich für alle drei Seiten des Dreiecks, dieselbe Konstruktionsfolge wiederholt, was für die Eingabe ermüdend ist. Jedoch gestattet der JSP-Generator sogar einen modularen Code mit JavaScript-Elementen, sodass der Generator-Quelltext für diese Konstruktion auch folgendermaßen lauten könnte:
function LabelSegment(segment,text,options) |
||
Die Funktion „LabelSegment“ wurde als allgemein nützliche Funktion auch in die Modul-Bibliothek ‚extensions.js‘ und ihre Kurzbeschreibung in die Code-Hilfedatei ‚help.htm‘ aufgenommen und steht damit wie viele andere nützliche Module jedem Generator-Code zur Verfügung.
2. Arbeit mit dem JSP-Generator

Die Arbeitsoberfläche des JSP-Generators besteht neben der oberen Steuerungsleiste aus dem linken Textfeld für den Generator-Code und dem rechten Textfeld für den aus dem Generator-Code erzeugten JSP-Code sowie für die Generator- und die Javascript-Hilfe. Nach Anklicken der Schaltfläche „Generator → JSP“ sowie der jetzt anstelle des Titels erscheinenden Schaltfläche „Applet starten“ wird das JSP-Applet gestartet und in einem eigenen Fenster angezeigt. Ist der Generator-Code fehlerhaft, so unterbleibt die Code-Konvertierung und in der Statusleiste erscheint die Meldung „Fehler auf der Seite“. Aber auch wenn der Generator-Code konvertiert wird, kann der JSP-Code manchmal Fehler enthalten. In diesem Fall bringt das Appletfenster eine Fehlermeldung.
Beim Eingeben des Generator-Codes können Sie sich viel Tipparbeit sparen, wenn Sie die gewünschten Syntaxelemente aus der zum Generator gehörigen Hilfedatei ‚help.htm‘, die nach Anklicken von „Hilfe“ im rechten Fenster angezeigt wird, zunächst markieren und dann entweder mit Strg+C und Strg+V oder per Drag-and-drop herauskopieren. Wenn Sie mit JavaScript-Strukturen arbeiten wollen, können Sie durch Anklicken von „JScript“ eine JavaScript-Hilfe (Autor: Stefan Münz; Website:SELFHTML) ins rechte Fenster holen.
Öffnen Sie nun den JSP-Generator und probieren Sie ihn aus, indem Sie einen der beiden oben stehenden Generator-Beispielcodes (nicht den JSP-Code!) in das Eingabefenster des Generators kopieren, ihn durch Anklicken von „Generator → JSP“ in den JSP-Code konvertieren und das Applet in der Titelleiste starten.
Falls Sie ‚Sichern‘ aktiviert haben, werden nach der Konvertierung des Generator-Codes in den JSP-Code zwei Dateien automatisch erzeugt und in Ihrem Download-Verzeichnis gespeichert: ‚<Projektname>.gen‘ und ‚<Projektname>.app‘. Die erstgenannte Datei enthält den erstellten Generator-Code, die zweite den Applet-Code, mit dem das JSP-Applet gestartet wird. Sie brauchen jetzt nur noch die oben vorgestellte HTML-Datei mit dem Applet-Code zu verlinken und haben damit bereits den Kern eines neuen elektronischen Arbeitsblatts kreiert.
Der gepackte JSP-Generator kann hier heruntergeladen werden.
Syntax von JavaSketchPad
1. Applet-Parameter
Unter Applet-Parametern versteht man Parameter, die beim Start eines Applets mit ihrer Bezeichnung („NAME“) aufgerufen und dann mit einem Wert („VALUE“) belegt werden, der eine bestimmte Eigenschaft des Applets festlegt. Im obenstehenden Quellcode haben Sie schon die Syntax einer solchen Parameterbelegung kennen gelernt:
<PARAM NAME="(Parameterbezeichnung)" VALUE="(Wert)">
Man unterscheidet zwischen allgemeinen, d. h. unabhängig von der aktuell vorliegenden Java-Anwendung gültigen Applet-Parametern und anwendungsspezifischen Applet-Parametern, die nur in der vorliegenden Anwendung einen Sinn machen. Hier eine kleine Übersicht über beide Parameter-Kategorien:
2. Konstruktionssyntax mit Übungsaufgaben
Wie das Beispiel eines HTML-Arbeitsblattes gezeigt hat, ist der gesamte Konstruktionstext von JavaSketchPad der Wert des Applet-Parameters "Construction". Der Text selbst ist zeilenweise aufgebaut, wobei jede Zeile genau einen Konstruktionsschritt enthält, der mit einem Strichpunkt abgeschlossen werden muss. In jedem Konstruktionsschritt wird ein Objekt (z. B. Punkt, Gerade, Kreis) meist mit Hilfe früherer (!) Objekte definiert, die anhand ihrer Zeilennummer in der Argumentliste des Objekts referenziert werden. So bedeutet z. B. die Zeile
Circle by radius ( 2 , 7 );
dass ein Kreis um den Punkt aus der Zeile 2 mit der Länge der Strecke aus der Zeile 7 als Radius gezeichnet wird, wobei diese Zeile selbst nach der 7. Zeile stehen muss.
Die Länge der Argumentliste eines Objekts ist genau festgelegt. Bei manchen Objekten ist aber auch ein Verweis auf eine variable Anzahl früherer Objekte nötig. In einem solchen Fall ist eine zusätzliche variable Argumentliste implementiert. Zum Beispiel steht bei dem Textobjekt "ConcatText" (Verknüpfung mehrerer Texte) nicht fest, wie viele Texte verknüpft werden sollen. Also werden nach der Platzierung des verknüpften Textes an den (xa; ya)-Punkt des Applet-Fensters die Referenz-Zeilennummern der zu verknüpfenden Textobjekte in eine variable zweite Argumentliste aufgenommen:
ConcatText ( xa , ya ) ( Nr_Text1 , Nr_Text2 , . . . ) ;
Es ist möglich, den Konstruktionstext mit Kommentaren zu versehen. Diese müssen allerdings in geschweiften Klammern stehen und werden dann vom JSP-Interpreter ignoriert. Die populärste Nutzung der Kommentierungsmöglichkeit besteht im zeilenweisen Voranstellen der aktuellen Zeilennummer, sodass der Applet-Verfasser leichter die Übersicht über die korrekte Objekt-Referenzierung behält. Beachten Sie, dass die Zeilennummernfolge lückenlos die natürlichen Zahlen durchläuft. Diesbezügliche Manipulationen bei den vorangestellten Zeilennummern haben auf die Zeilenzählung von JavaSketchPad keinerlei Einfluss, da Kommentare ja ohnehin ignoriert werden! Der nachträgliche Einschub einer Zeile ist daher immer schmerzhaft, da er die Korrektur aller bereits vorhandenen nachfolgenden Referenzen auf Objekte erforderlich macht, die zwischen der eingeschobenen Zeile und der referenzierenden Zeile stehen.
Diese (wohl bei jeder Erstellung eines JSP-Applets irgendwann erforderliche) Referenznummern-Korrektur enfällt, wenn man den im letzten Kapitel eingeführten JSP-Generator benutzt. Sein Schöpfer Hans Klein hat die Syntax von JavaSketchPad so abgeändert, dass sie voll JavaScript-tauglich geworden ist und sogar eine modulare Struktur erlaubt. Die Zeilennummern-Referenzierung ist hier durch die Verwendung von Variablen überflüssig gemacht worden, sodass der nachträgliche Einschub eines Konstruktionsschritts kein Problem darstellt. Ein eingebauter Konverter verwandelt diese Generator-Syntax wieder in herkömmliche JSP-Syntax, die dann automatisch in eine HTML-Datei geschrieben und als JSP-Applet gestartet wird. In der Excel-Datei „Jsp.xls“ sind die Syntax-Elemente von JavaSketchPad und vom JSP-Generator parallel zueinander aufgelistet und kommentiert.
Leider enthält JavaSketchPad keine benutzerfreundliche Fehlerbehandlung. Selbst die Groß- und Kleinschreibung in seiner Syntax ist genauestens zu beachten. Auch der kleinste Fehler (z. B. ein missbräuchliches Verwenden des Strichpunkts in einem Text) wird ohne jeden Fehlerhinweis rigoros durch Nichtstarten des Applets bestraft. Zur Vermeidung einer endlosen Fehlersuche hilft nur zeilenweises Testen mit dem Browser.
Die vollständige Syntax von JavaSketchPad ist in den folgenden Tabellen nach Objektfamilien geordnet aufgelistet. In der ersten Tabellenspalte steht der Objektbegriff, in der zweiten Spalte die JSP-Syntax dazu, und in der dritten Spalte werden die Argumentlisten kurz erläutert. Eine genauere (englischsprachige) Information zu jedem Objekt lässt sich durch Anklicken des jeweiligen JSP-Begriffs in der zweiten Spalte erhalten.
Den einzelnen Objektfamilien sind Übungsaufgaben beigefügt, die mit Hilfe des JSP-Generators bearbeitet werden können. Zu diesen Übungsaufgaben sind Musterlösungen hinterlegt:
| Übungsaufgabe | Musterlösung |
| 01_Punkte_Linien.gen | 01_Punkte_Linien_Lsg.gen |
| 02_Kreise_Flaechen.gen | 02_Kreise_Flaechen_Lsg.gen |
| 03_Bilder.gen | 03_Bilder_Lsg.gen |
| 04_Masse.gen | 04_Masse_Lsg.gen |
| 05_Gitternetze.gen | 05_Gitternetze_a_Lsg.gen |
| 05_Gitternetze_b_Lsg.gen | |
| 05_Gitternetze_c_Lsg.gen | |
| 05_Gitternetze_d_Lsg.gen | |
| 05_Gitternetze_e_Lsg.gen | |
| 06_geo_Ort.gen | 06_geo_Ort_Lsg.gen |
| 07_Graph.gen | 07_Graph_a_Lsg.gen |
| 07_Graph_b_Lsg.gen | |
| 08_Abbildungen.gen | 08_Abbildungen_Lsg.gen |
| 08_Abbildungen_Lsg_modul.gen | |
| 09_Buttons.gen | 09_Buttons_1_Lsg.gen |
| 09_Buttons_2_Lsg.gen | |
| 09_Buttons_3_Lsg.gen | |
| 10_Animationen.gen | 10_Animationen_1_Lsg.gen |
| 10_Animationen_2_Lsg.gen |
| 2.1 |
Punktobjekte Syntax im JSP-Generator |
||||||||||||||||||||||||||||||||||||||||||
Freie Punkte sind mit der Maus verschiebbar, feste Punkte nicht.
|
|||||||||||||||||||||||||||||||||||||||||||
| 2.2 |
Textobjekte Syntax im JSP-Generator |
||||||||||||||||||||||||||||||||||||||||||
Ein Text kann entweder mit FixedText direkt oder auch mit Maßobjekten (s.u.) definiert werden. Im letzteren Fall besteht ein Text aus dem Maß (Wert) eines geometrischen Objekts sowie einem eventuellen Textvorspann oder Textnachspann, der zusammen mit dem Maßobjekt definiert wird.
|
|||||||||||||||||||||||||||||||||||||||||||
| 2.3 |
Linienobjekte Syntax im JSP-Generator |
||||||||||||||||||||||||||||||||||||||||||
Bei den Linienobjekten „Segment“, „Line“ und „Ray“ ist der zweitgenannte Punkt der Startpunkt und der erstgenannte Punkt der Zielpunkt. Diese scheinbar nur für „Ray“ sinnvolle Aussage ist insofern auch für die beiden anderen Linienobjekte bedeutsam, als bei der Gleiterdefinition mit „Point on object“ der Positionswert 0 sich stets auf den Startpunkt und der Positionswert 1 sich auf den Zielpunkt bezieht.
|
|||||||||||||||||||||||||||||||||||||||||||
| 2.4 |
Kreisobjekte Syntax im JSP-Generator |
||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||
| 2.5 |
Flächenobjekte Syntax im JSP-Generator |
||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||
| 2.6 |
Bildobjekte Syntax im JSP-Generator |
||||||||||||||||||||||||||||||||||||||||||
JavaSketchPad erlaubt die Einbindung von Bilddateien in das Appletfenster. Der entweder mittels Applet-Koordinaten oder mittels Punktobjekten anzugebende Ort stellt dann die linke obere Ecke des Bildes dar. Der Pfad der Bilddatei muss immer relativ zum CodeBase-Verzeichnis, also zu dem Verzeichnis, das das JSP-Archiv 'jsp4.jar' enthält, angegeben werden. Außerdem muss die Bilddatei aus Sicherheitsgründen entweder im CodeBase-Verzeichnis oder in einem Unterverzeichnis davon liegen!
|
|||||||||||||||||||||||||||||||||||||||||||
| 2.7 |
Maßobjekte Syntax im JSP-Generator |
||||||||||||||||||||||||||||||||||||||||||
Maßobjekte geben eine geometrische Maßzahl aus. Der Ort dieser Ausgabe wird mit den in der Argumentliste enthaltenen Applet-Koordinaten festgelegt. Damit die Maßzahl nicht völlig isoliert erscheint, besteht die Möglichkeit der Eingabe eines Textvorspanns (letztes, bei 'Calculate' vorletztes Argument) sowie des Hinzufügens eines Textnachspanns (s. Objektformatierung: Formatierung von Maß- und Textobjekten weiter unten). Für Berechnungen dient das Maßobjekt „Calculate“, das in seiner ersten (festen) Argumentliste einen Rechenterm enthält. Der Aufbau dieses Terms muss nach der umgekehrten polnischen Notation erfolgen, die ohne Klammern auskommt. Z. B. lautet der Term '
|
|||||||||||||||||||||||||||||||||||||||||||
| 2.8 |
Gitternetzobjekte Syntax im JSP-Generator |
||||||||||||||||||||||||||||||||||||||||||
Beachten Sie, dass die Konstruktion eines der ersten beiden Gitternetzobjekte nicht automatisch die Achsen einschließt. Diese müssen im Bedarfsfall eigens konstruiert werden (s. Linienobjekte)!
|
|||||||||||||||||||||||||||||||||||||||||||
| 2.9 |
Ortsobjekt Syntax im JSP-Generator |
||||||||||||||||||||||||||||||||||||||||||
Funktionsgraphen können mit „Locus“ folgendermaßen dargestellt werden: { 1} Point(250,275); {Ursprung z. B. bei (250,275) definieren}
{ 2} UnitPoint(1,50); {beweglicher Einheitspunkt z. B. 50 Pixel rechts vom Ursprung}
{ 3} RectangularUnitPoint(2,50); {2. beweglicher Einheitspunkt z. B. 50 Pixel über dem Ursprung}
{ 4} HorizontalAxis(1,2); {x-Achse}
{ 5} VerticalAxis(1,3); {y-Achse}
{ 6} CoordSysByAxes(4,5); {Koordinatensystem}
{ 7} Point on object(4,0.5)[hidden]; {Gleiter auf x-Achse}
{ 8} Ratio/Points(1,2,7,0,0,'')[hidden]; {x-Koordinate des Gleiters}
{ 9} Calculate(0,0,'','A2^')(8)[hidden]; {y = f(x), z. B. y = x2, umgekehrte polnische Notation!}
{10} PlotXY(9,6,8)[hidden]; {Graphenpunkt (x | f(x))}
{11} Locus(10,7,4,200); {Ortskurve des Graphenpunktes}
|
|||||||||||||||||||||||||||||||||||||||||||
| 2.10 |
Abbildungsobjekte Syntax im JSP-Generator |
||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||
| 2.11 |
Schaltflächenobjekte Syntax im JSP-Generator |
||||||||||||||||||||||||||||||||||||||||||
MoveButton erfordert im Gegensatz zu AnimateButton keine „Bahn“ für den/die bewegten Punkt/e. SimultaneousButton simuliert das gleichzeitige Betätigen mehrerer Schaltflächen.
|
3. Objektformatierung Syntax im JSP-Generator
Schon im Beispiel-Quellcode haben Sie gesehen, dass zwischen der Konstruktionsanweisung und dem Strichpunkt am Zeilenende im Regelfall noch ein Ausdruck in eckigen Klammern steht. Dieser (stets optionale) Ausdruck enthält Formatierungsanweisungen für das aktuelle Konstruktionsobjekt, die mit Kommata getrennt werden. Fehlt der Formatierungsausdruck, so wird das Objekt in dem von JSP voreingestellten Format dargestellt.
| 3.1 |
Allgemeine Formatierungsmöglichkeiten |
||||||||||||||||||
|
|||||||||||||||||||
| 3.2 |
Formatierung von Punktobjekten |
||||||||||||||||||
|
|||||||||||||||||||
| 3.3 |
Formatierung von Maß- und Textobjekten |
||||||||||||||||||
|
|||||||||||||||||||
| 3.4 |
Formatierung von Schaltflächenobjekten |
||||||||||||||||||
|
Weitere Übungsaufgaben mit dem JSP-Generator
1. Übungsaufgabe
Es soll ein Applet erstellt werden, das empirisch belegt, dass die Innenwinkelsumme im Dreieck 180º beträgt. Dabei sollen die drei farblich unterschiedlich und mit variablem Radius markierten und beschrifteten Innenwinkel durch Verschiebung bzw. Spiegelung an der Dreiecksspitze so aneinander gereiht sein, dass ihre Summe direkt ersichtlich ist.
Das fertige Produkt könnte dann etwa folgendermaßen aussehen:
|
Die Innenwinkel α, β und γ des nebenstehenden Dreiecks sind durch Verschiebung bzw. Spiegelung an der Dreiecksspitze zusammengestellt worden.
Was fällt Ihnen in Bezug auf die Summe dieser drei Winkel auf?
Bestätigen Sie Ihre Vermutung, indem Sie mit der Maus die drei Ecken des Dreiecks verschieben und dabei weiter die an der Dreiecksspitze dargestellte Winkelsumme beobachten!
Initialisieren Sie das Applet durch Drücken der Taste ' r '. |
|
Öffnen Sie nun die Datei ‚Uebung1.gen‘, die die Anleitung zur Erstellung des Generator-Codes für dieses Applet enthält. Kopieren Sie den gesamten Text in das linke Fenster des JSP-Generators. Tragen Sie anschließend zeilenweise nach dem Kommentar-Ende */ unter Zuhilfenahme der Code-Hilfe und des Drag-and-drop-Verfahrens die einzelnen Konstruktionsschritte im Generator-Code ein. Beginnen Sie mit dem Hauptprogramm (nicht mit der Funktion). Zur besseren Kontrolle verzichten Sie zunächst darauf, falls gefordert, Objekte zu verstecken, und holen Sie das später nach. Klicken Sie nach jedem Konstruktionsschritt auf die Schaltfläche „Generator → JSP“ und dann auf „Applet starten“ und überzeugen Sie sich von der Fehlerfreiheit Ihrer Eingabe. Die Lösung dieser Aufgabe ist in der Datei ‚Uebung1_Lsg.gen‘ zu finden.
Wenn Sie mit der gesamten Konstruktion fertig sind, geben Sie ihr den Projektnamen „Uebung1“, legenn Sie ggf. die Breite und Höhe des Applets fest und aktivieren Sie vor der Code-Konvertierung „Sichern“ durch einen Mausklick. Im Downloads-Verzeichnis finden Sie nun Ihre erstellte JSP-Applet-Datei „Uebung1.app“. Verschieben Sie diese Datei in das Unterverzeichnis „Uebungen“ zu dieser Anleitung. Damit wird die bereits vorhandene Datei gleichen Namens überschrieben. Öffnen Sie nun die Arbeitsblatt-Vorlage Uebung1.htm und starten Sie durch Klicken auf „Applet starten“ Ihr erstelltes Applet.
(Zum Vergleich: Uebung1_Lsg.htm)
2. Übungsaufgabe
Es soll ein Applet mit Koordinatensystem erstellt werden, in dem die (rote) Normalparabel y = x2 mit einem Parabelpunkt P und der (schwarzen) Parabeltangente durch P dargestellt wird. Der Punkt P soll mit Hilfe eines Schiebers auf einer waagrechten (schwarzen) Schiene im unteren Teil des Applets verstellbar sein. Der Benutzer soll entscheiden können, ob die mitwandernde Tangente eine Spur hinterlässt oder nicht, und auch zwischen beiden Möglichkeiten hin- und herschalten können. Außerdem soll der Schieber animierbar sein, sodass sich dann der Punkt P mitsamt seiner Tangente automatisch bewegt. Dem Applet sollen passende Arbeitsaufträge beigefügt werden.
Das fertige Produkt könnte dann etwa folgendermaßen aussehen:
|
Verschieben Sie den roten Gleiter auf der unteren grauen Schiene! Was beobachten Sie? Lesen Sie die Steigungen der
Normalparabel an den folgenden
Stellen ab: Stellen Sie die Tangente mit der Steigung m = 1 ein. Welche Abszisse hat der Berührpunkt? Welcher Bereich wird von keiner
Tangente geschnitten?
Initialisieren Sie das Applet durch Drücken der Taste ' r '. |
|
Öffnen Sie diesmal die Datei ‚Uebung2.gen‘ und verfahren Sie wie in Beispiel 1. Die Lösung dieser Aufgabe ist in der Datei ‚Uebung2_Lsg.gen‘ zu finden. Öffnen Sie auch diesmal die zugehörige Arbeitsblatt-Vorlage Uebung2.htm und starten Sie durch Klicken auf „Applet starten“ Ihr erstelltes Applet.
(Zum Vergleich: Uebung2_Lsg.htm)
Modul-Bibliothek zum JSP-Generator
1. Markierung eines Winkels
Autor (Name, Dienststelle, evtl. email):
Peter Starfinger, BOS Sozialwesen München, Peter.Starfinger@gmx.de
Aufruf:
MarkAngle(A,S,B,r,n,txt,opt_legs,opt_sector,opt_arc,opt_txt)
Leistung:
Diese Funktion stellt den Winkel ASB dar und beschriftet ihn mit txt (Stil: opt_txt). Sie zeichnet die Schenkel SA and SB (Stil: opt_legs), einen Kreissektor (eigentlich ein Polygon mit n+2 Ecken) mit einem Radius, der der Länge der Strecke r entspricht. Sie färbt den Sektor ein (Stil: opt_sector) und zeichnet den zugehörigen Kreisbogen (Stil: opt_arc). Der voreingestellte Wert für den Parameter 'DirectedAngles' im Aufruf des Applets muss 1 sein.
Quellcode:
function MarkAngle(A,S,B,r,n,txt,opt_legs,opt_sector,opt_arc,opt_txt) {
var acc_sector = ','
var acc_txt = ','
if (opt_sector == '') acc_sector = ''
if (opt_txt == '') acc_txt = ''
var s1 = Ray(A,S,opt_legs)
var s2 = Ray(B,S,opt_legs)
var kS = Circle_by_radius(S,r,'hidden')
var S1 = Intersect2(s1,kS,'hidden')
var S2 = Intersect2(s2,kS,'hidden')
var rad=Angle(A,S,B,10,10,'','hidden')
rad=Calculate(10,30,'',Math.PI+' 2*A+',[rad],'hidden')
rad=Calculate(10,50,'','AA2 '+Math.PI+'*/@trnc2*'+Math.PI+'*-',[rad],'hidden')
var rad_n=Calculate(10,50,'','A'+n+'/',[rad],'hidden')
var S_ = new Array(n+2)
S_[0] = S1
for (var i=1; i<n; i++)
{S_[i] = RotationMeasuredAngle(S_[i-1],S,rad_n,'hidden')
Segment(S_[i],S_[i-1],opt_arc)}
S_[n] = S2
Segment(S_[n],S_[n-1],opt_arc)
S_[n+1] = S
Polygon(S_,'layer(1)'+acc_sector+opt_sector)
var rad_2=Calculate(10,50,'','A2/',[rad],'hidden')
var S_2=RotationMeasuredAngle(S1,S,rad_2,'hidden')
var M=Dilation(S_2,S,0.6,'hidden')
var T = FixedText(0,0,txt,'hidden')
PeggedText(M,T,'justifyCenter'+acc_txt+opt_txt)
}
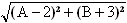 ' in der umgekehrten polnischen Notation: 'A2-2^B3+2^+@sqrt', d. h. der Operator (+; -; *; /; ^; @sqrt usw.) steht erst nach den Operanden. Sind diese keine Platzhalter, sondern Zahlen, so werden sie durch ein Leerzeichen getrennt: '2²*3.14' wird also zu '2 2^3.14*'. Für die Vorzeichenfunktion, die Betragsfunktion, die Wurzelfunktion, die Rundungsfunktionen sowie die transzendenten Funktionen (trigonometrische Funktionen mit Bogenmaß-Argumenten!) steht das Symbol '@xxxx' zur Verfügung: @sgn_; @abs_; @sqrt; @rond; @trnc; @sin_; @cos_; @tan_; @asin; @acos; @atan; @ln__; @log_. Dem Klammeraffen müssen also 4 Zeichen folgen; ggf. wird mit dem Unterstrich '_' aufgefüllt.
' in der umgekehrten polnischen Notation: 'A2-2^B3+2^+@sqrt', d. h. der Operator (+; -; *; /; ^; @sqrt usw.) steht erst nach den Operanden. Sind diese keine Platzhalter, sondern Zahlen, so werden sie durch ein Leerzeichen getrennt: '2²*3.14' wird also zu '2 2^3.14*'. Für die Vorzeichenfunktion, die Betragsfunktion, die Wurzelfunktion, die Rundungsfunktionen sowie die transzendenten Funktionen (trigonometrische Funktionen mit Bogenmaß-Argumenten!) steht das Symbol '@xxxx' zur Verfügung: @sgn_; @abs_; @sqrt; @rond; @trnc; @sin_; @cos_; @tan_; @asin; @acos; @atan; @ln__; @log_. Dem Klammeraffen müssen also 4 Zeichen folgen; ggf. wird mit dem Unterstrich '_' aufgefüllt.